Cách chứng minh hình bình hành? Tính chất của hình bình hành? Hình bình hành là hình gì? Hôm nay Vimi sẽ chia sẻ với các bạn học sinh “bí kíp” làm dạng bài này nắm chắc điểm 10 trong tay.
1. Hình bình hành là gì?
Trước khi tìm hiểu cách chứng minh hình bình hành, cùng đến với khái niệm về hình bình hành nhé.
📌 Hình bình hành tên tiếng anh là Parallelogram là một hình thang có dạng đặc biệt với hai cạnh bên song song. Hay còn gọi là một tứ giác có các cạnh đối song song với nhau. Đây là một dạng hình học thông dụng thường xuất hiện trong lĩnh vực toán học và kỹ thuật hiện nay.

2. Dấu hiệu nhận biết cơ bản của hình bình hành
Để biết cách chứng minh hình bình hành, cần nắm được một số tính chất cơ bản của hình bình hành như:
✔ Các cặp cạnh đối song song và bằng nhau.
✔ Các góc trong hình đối nhau và bằng nhau.
✔ Tại trung điểm mỗi đường, 2 đường chéo cắt nhau, gọi là tâm đối xứng của hình bình hành.
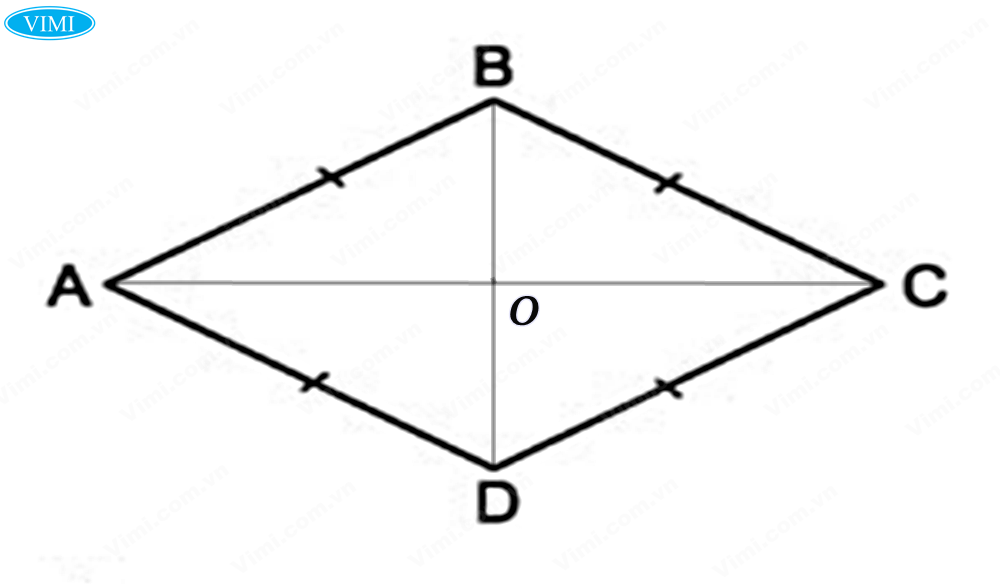
2.1. Khi bạn cần chứng minh 1 hình tứ giác là hình bình hành
Cách chứng minh hình bình hành thông qua 1 tứ giác là gì?
Khi đề bài cho một hình tứ giác, hãy nhìn vào những dấu hiệu dưới đây để nhận biết hình bình hành:
✔ Có hai cặp cạnh đối nhau, song song và bằng nhau.
✔ Có hai cạnh của tứ giác đối nhau, song song và bằng nhau.
✔ Có hai cặp góc của hình tứ giác đối nhau và bằng nhau.
✔ Hai đường chéo của tứ giác cắt nhau tại trung điểm mỗi đường.
2.2. Khi hình bình hành tồn tại ở dạng hình thang
Cách chứng minh hình bình hành thông qua 1 hình thang là gì?
Khi đề bài cho một hình thang, hãy nhìn vào những dấu hiệu dưới đây để nhận biết hình bình hành:
✔ Khi hình thang có cặp cạnh đáy bằng nhau.
✔ Khi hình thang có cặp cạnh hai bên song song với nhau.
Với những dấu hiệu đó, chúng ta sẽ dễ dàng liên tưởng đến các hình như: hình chữ nhật, hình vuông, hình thoi – đó là các hình dạng đặc biệt của hình bình hành. Chỉ cần bám sát vào các dấu hiệu sẽ rất dễ để nhận biết.
Vimi là đơn vị chuyên cung cấp các sản phẩm van công nghiệp (van bướm, van cổng, van giảm áp…), các sản phẩm thiết bị đo (đồng hồ áp suất, đồng hồ nhiệt độ…), phụ kiện inox (mặt bích inox, tê inox, lơ thu inox…), chúng tôi không chỉ chia sẻ các kiến thức chủ đạo về sản phẩm và dịch vụ mà bên cạnh đó cũng có cả các kiến thức mở rộng, quý bạn đọc có thể tìm hiểu thêm tại Blog Vimi.
3. Cách chứng minh hình bình hành
Khi chứng minh một tứ giác là hình bình hành, đầu tiên các bạn cần nắm chắc các dấu hiệu nhận biết của hình bình hành. Vì đó là những yếu tố quan trọng mà chúng ta sẽ bám sát trong quá trình làm bài. Hoặc chúng ta sẽ sử dụng dạng đặc biệt, chứng minh hình thang sau đó thông qua những dấu hiệu của hình bình hành trong hình thang để chứng minh.
3.1. Chứng minh tứ giác là hình bình hành khi có 2 cặp cạnh đối song song
Cách chứng minh hình bình hành thông qua 1 tứ giác có 2 cặp cạnh đối song song là gì?
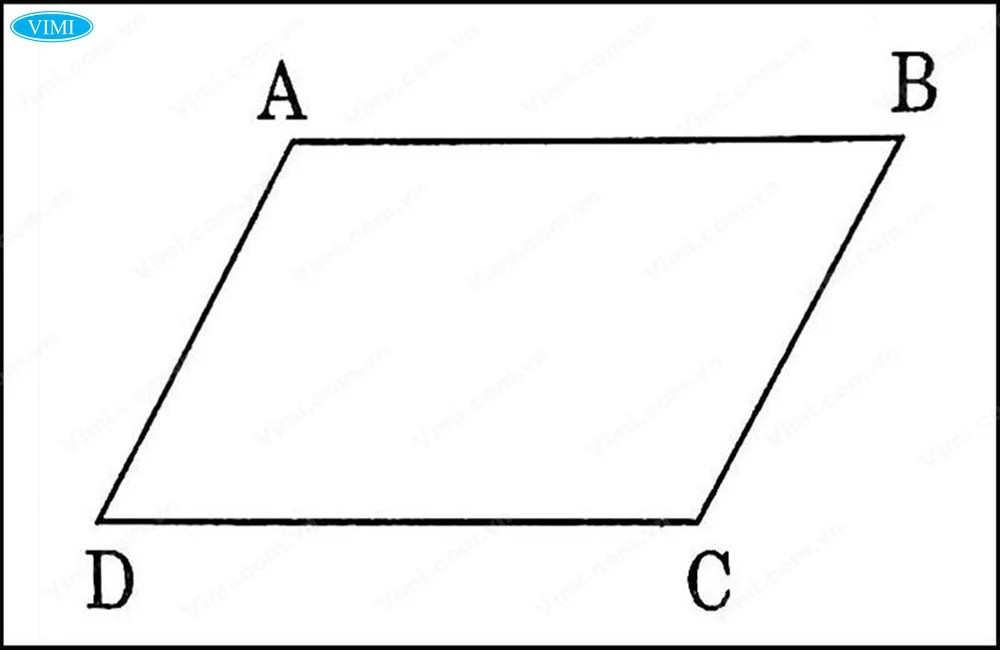
✔ Cho hình bình hành ABCD. Có AB // DC & AD // BC <=> ABCD là hình bình hành (theo tính chất các cặp cạnh đối song song với nhau).
3.2. Chứng minh tứ giác là hình bình hành khi có 2 cặp cạnh đối bằng nhau
Cách chứng minh hình bình hành thông qua 1 tứ giác có 2 cặp cạnh đối bằng nhau là gì?
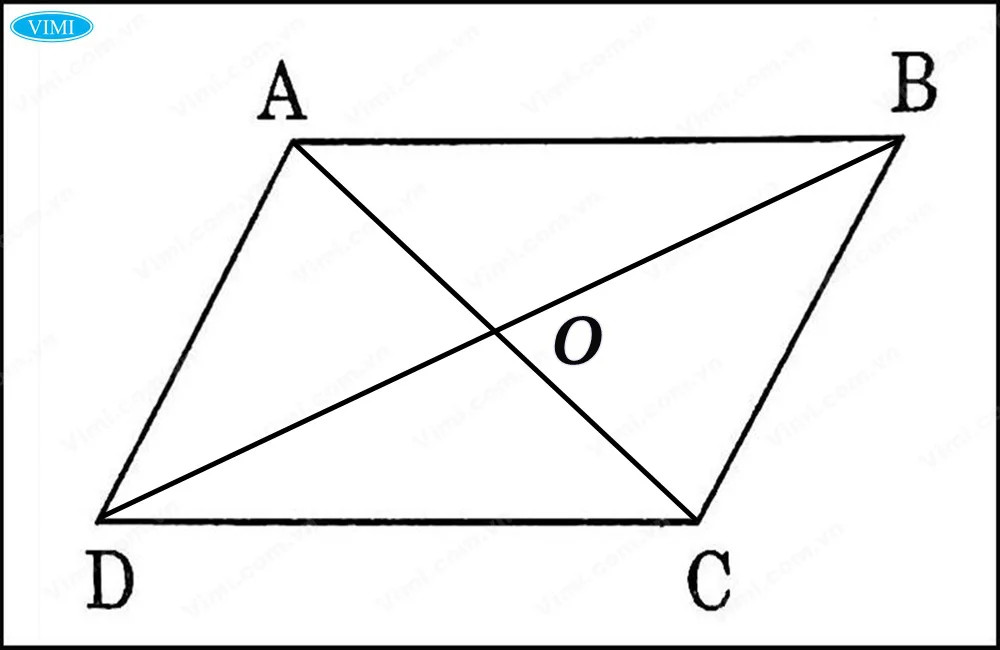
✔ Cho tứ giác ABCD. 2 đường chéo AC và BD cắt nhau tại O. Có tam giác ABC và tam giác ADC:
- AD = BC
- AB = CD
✔ Trong đó, cạnh chung giữa hai tam giác là AC => Tam giác ABC = tam giác ADC (theo tính chất cạnh.cạnh.cạnh)
✔ Khi hai tam giác bằng nhau, ta có:
- Góc BAC = góc DAC (góc tương ứng). 2 góc này ở vị trí so le trong => BC // AD (1)
- Góc CAB = góc ACD (góc tương ứng). 2 góc này ở vị trí so le trong => DC // AB (2)
✔ Từ (1) và (2), ta có tứ giác ABCD là hình bình hành.
3.3. Chứng minh tứ giác có cặp cạnh đối song song và bằng nhau là hình bình hành
Cách chứng minh hình bình hành thông qua 1 tứ giác có cặp cạnh đối song song và bằng nhau là gì?
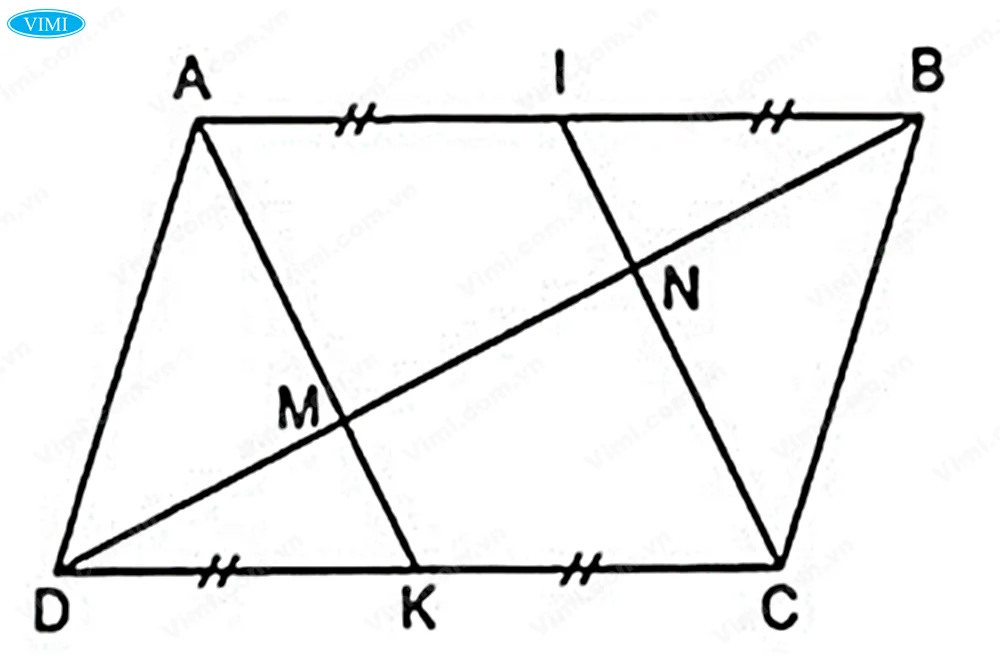
✔ Từ định nghĩa, tính chất của hình bình hành, ta có:
- AB // CD
- AB = CD
- AI = IB
- DK = KC
=> AI // KC và AI = KC
3.4. Chứng minh tứ giác có 2 cặp góc đối bằng nhau là hình bình hành
Cách chứng minh hình bình hành thông qua 1 tứ giác có 2 cặp góc đối bằng nhau là gì?
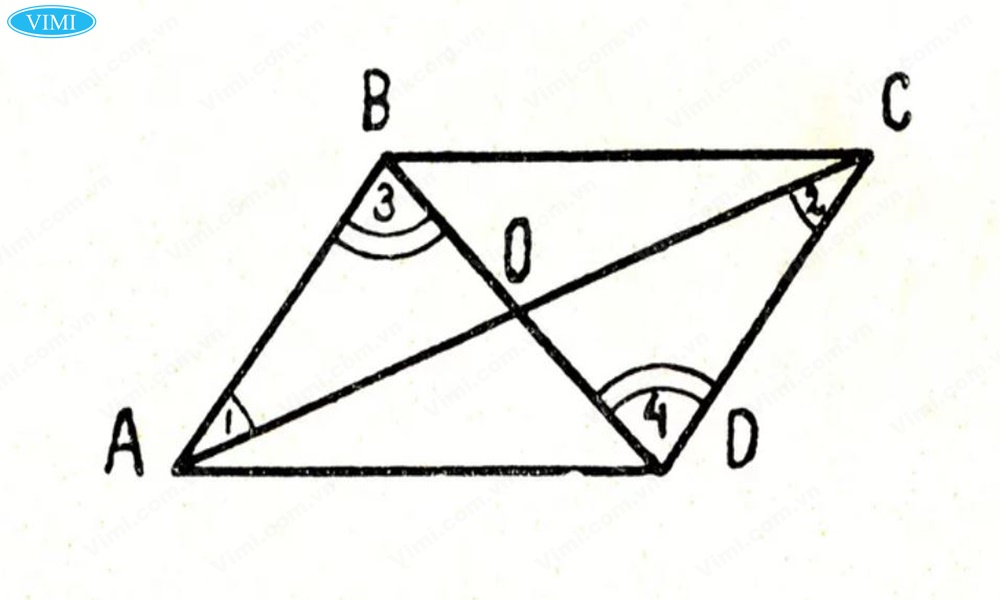
✔ Cho tứ giác ABCD có tam giác ABD = tam giác BCD & tam giác ABC = tam giác ADC.
✔ Ta có:
- Tam giác BCD = tam giác BAD (theo lý thuyết) => góc BCD = góc BAD (1)
- Tam giác ABC = tam giác ADC (theo lý thuyết) => góc ABC = góc ADC (2)
✔ Từ (1) và (2), do các góc đối bằng nhau nên ta chứng minh được tứ giác ABCD là hình bình hành.
3.5. Chứng minh tứ giác có hai đường chéo cắt nhau tại trung điểm là hình bình hành
Cách chứng minh hình bình hành thông qua 1 tứ giác có 2 đường chéo cắt nhau tại trung điểm là gì?
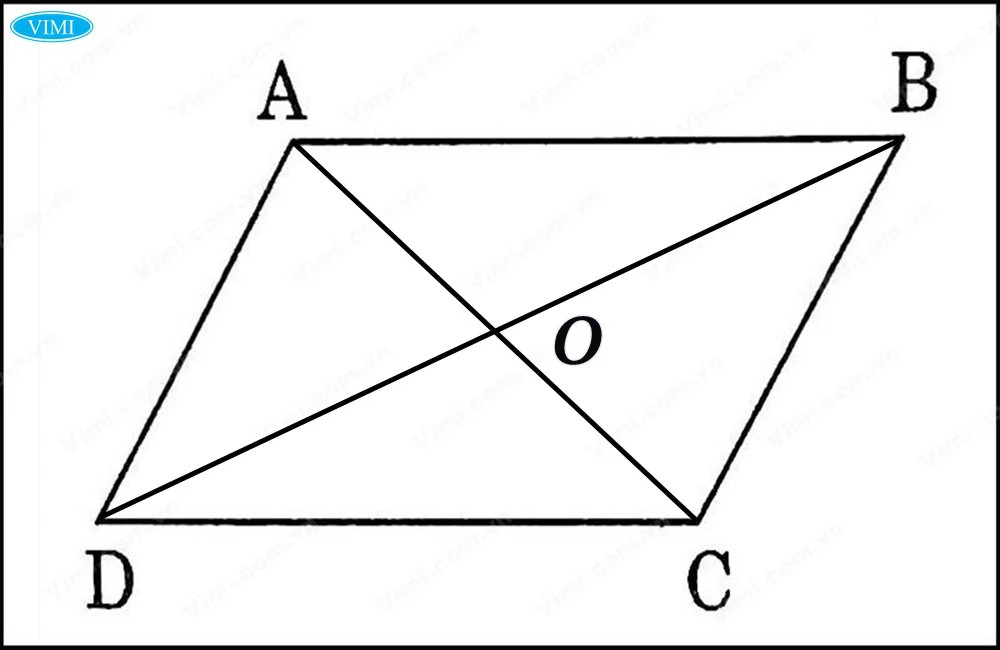
✔ Tứ giác ABCD có AC cắt BD tại O => O là trung điểm của AC và BD.
Ta có OA=OC và OB=OD.
✔ Xét tam giác AOD và tam giác COB có:
- OA = OC
- Góc AOD = góc BOC (đối đỉnh)
- OB = OD
=> tam giác AOD = tam giác COB (theo tính chất cạnh – góc – cạnh)
- => AD = BC (1).
- Góc DAO = góc BCO => AD // BC (2)
✔ Từ (1) và (2) => tứ giác ABCD là hình bình hành.
4. Các dạng bài tập về hình bình hành
Hình bình hành có các dạng bài từ cơ bản đến nâng cao. Để làm được các dạng bài tập về cách chứng minh hình bình hành, các bạn học sinh cần nắm vững lý thuyết cũng như tính chất của hình bình hành, làm nhuần nhuyễn các dạng bài cơ bản trước.
Dạng 1: Ứng dụng tính chất của hình bình hành để chứng minh các tiên đề liên quan
✔ Phương pháp: Bám sát vào lý thuyết nhận biết dấu hiệu trong hình bình hành về góc, cạnh, đường chéo, các tính chất song song và bằng nhau từ đó chứng minh được các tính chất hình học khác.
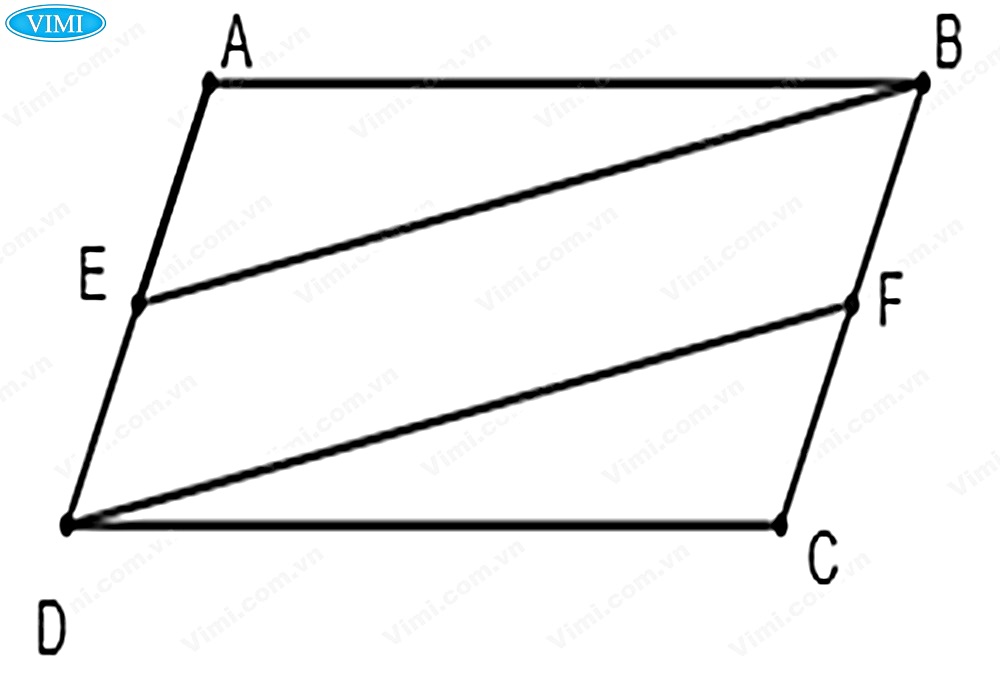
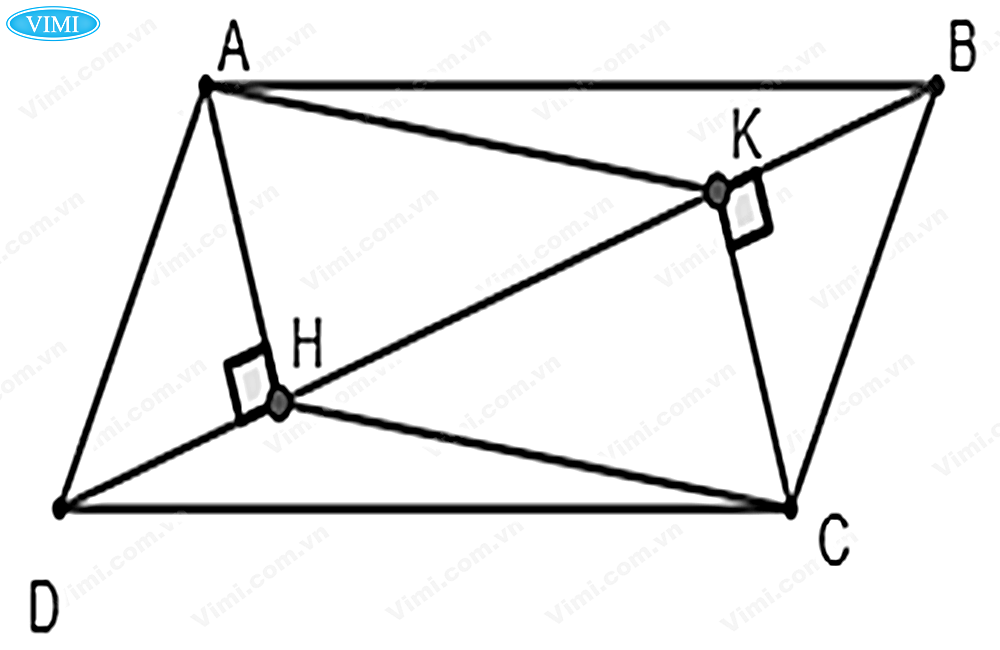
Dạng 2: Chứng minh một tứ giác là hình bình hành
Cách chứng minh hình bình hành thông qua 1 tứ giác là gì?
✔ Phương pháp: Sử dụng chặt chẽ các dấu hiệu nhận biết trong hình và các hình dạng đặc biệt của hình bình hành để chứng minh.
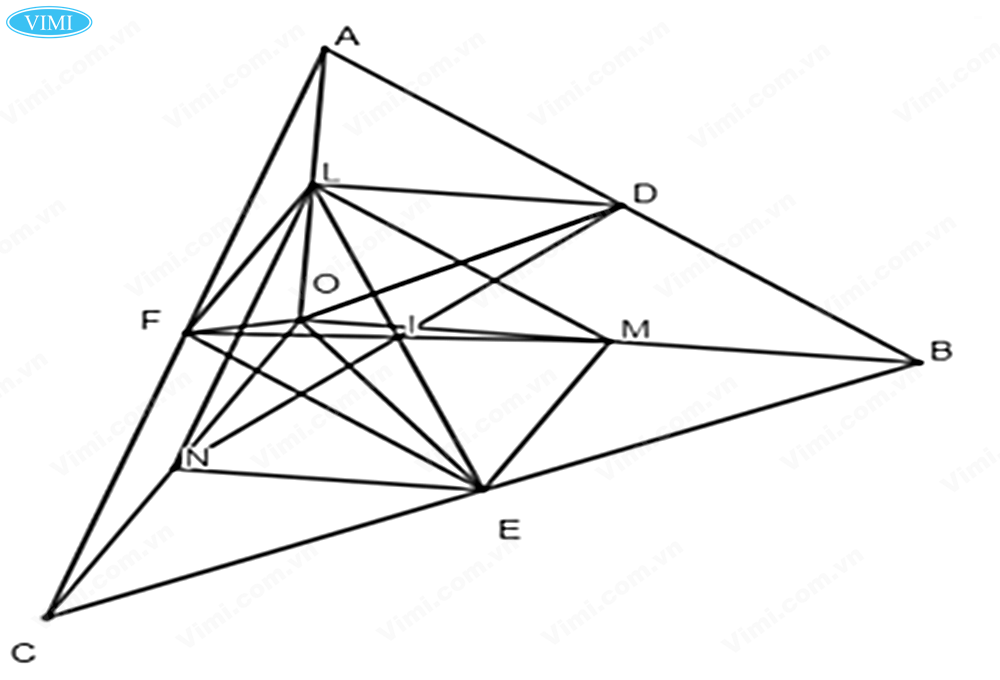
Dạng 3: Chứng minh 3 đường thẳng đồng quy, 3 điểm thẳng hàng.
Cách chứng minh hình bình hành thông qua chứng minh 3 đường thẳng đồng quy, 3 điểm thẳng hàng là gì?
✔ Phương pháp: Áp dụng các tính chất về đường chéo và tâm đối xứng của hình bình hành.
=> Dù là dạng cơ bản hay nâng cao cũng đòi hỏi người làm có nền tảng kiến thức vững chắc để dễ dàng áp dụng và chứng minh mở rộng.
5. Cách tính chu vi, diện tích hình bình hành
Ngoài cách chứng minh hình bình hành, bạn đọc có thể tham khảo cách tính chu vi và tính diện tích hình bình hành ngay dưới đây:
5.1. Chu vi hình bình hành
✔ Chu vi một hình bình hành sẽ bằng C = (a+b) x 2 (tức là 2 lần tổng của một cặp cạnh bất kỳ kề nhau), (C là kí hiệu chu vi).
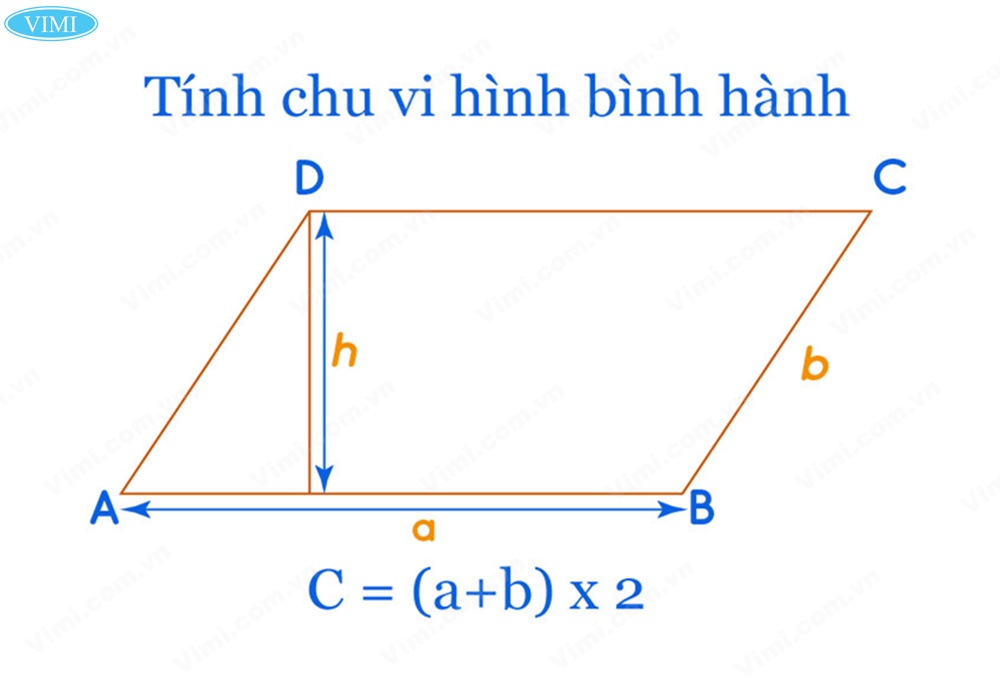
5.2. Diện tích hình bình hành
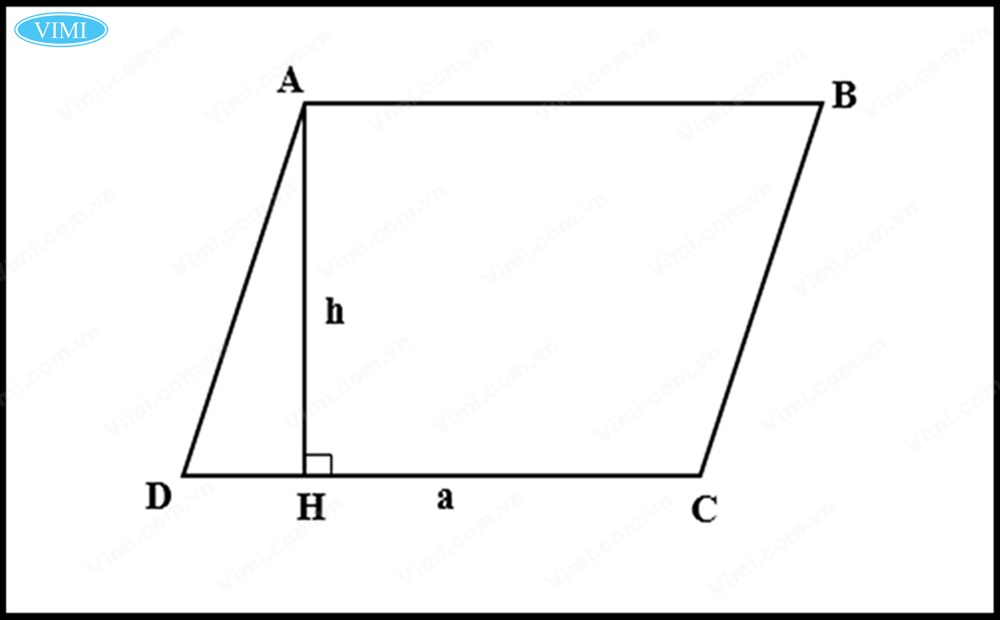
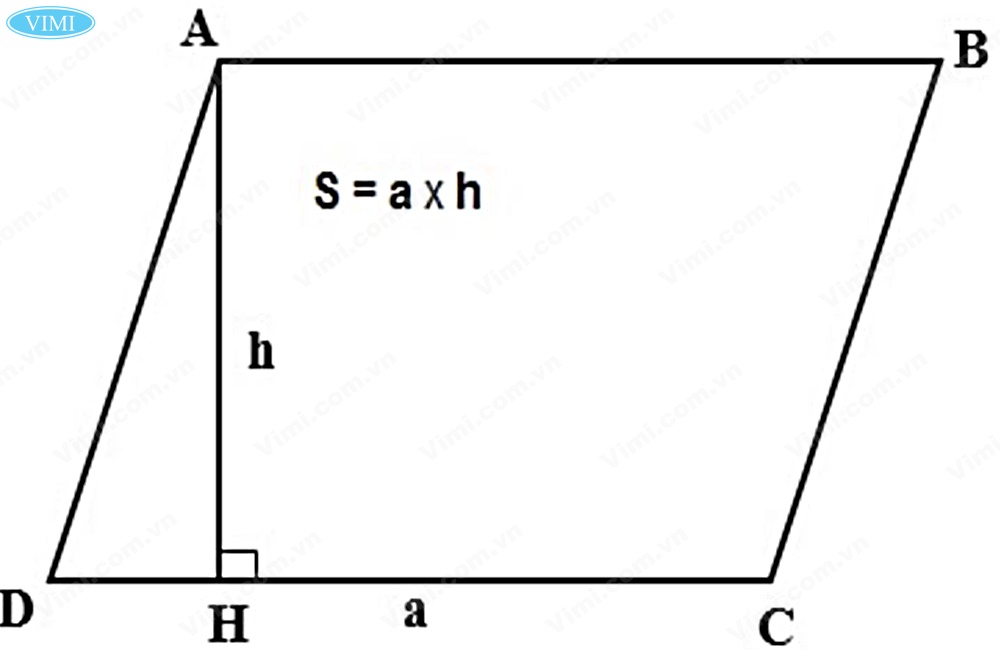
✔ Diện tích một hình bình hành sẽ bằng S = B x H trong đó:
- B là độ dài cạnh đáy.
- H là độ dài của chiều cao.
- S là kí hiệu diện tích.
6. Một số lưu ý khi chứng minh hình bình hành
Bất cứ một loại hình học nào cũng có những dấu hiệu và tính chất riêng biệt, hình bình hành cũng vậy. Để biết cách chứng minh hình bình hành, bạn cần nắm chắc các tính chất và lưu ý 1 số điều sau đây sẽ giúp cho các bạn học sinh làm các bài tập hình học đơn giản và nhanh chóng hơn nhiều.

✔ Khi nhìn thấy đề bài, hãy tập thói quen vẽ hình, phác thảo hình ảnh theo đề sẽ giúp bạn hình dung một cách nhanh chóng hơn phương hướng giải.
✔ Khi vẽ được hình là bạn đã giải quyết được 50% bài toán, sau đó hãy dựa vào các kiến thức lý thuyết nhận biết dạng hình học và các tính chất liên quan giúp bạn chứng minh.
✔ Đừng học lý thuyết một cách máy móc và giải đề một cách cứng nhắc, hãy coi lý thuyết là nền tảng và linh hoạt, sáng tạo trong phương pháp giải sẽ giúp bạn giải được các dạng bài tập khác nhau.
✔ Hãy học cách chứng minh hình bình hành khoa học, đầy đủ các bước dựa trên hình vẽ sao cho người đọc nhìn vào cảm thấy dễ hiểu, dễ chịu. Viết tắt quá nhiều hay làm quá sơ sài sẽ khiến bài của bạn bị trừ điểm đấy!
Chúc các bạn giành được những điểm số cao trong học tập!
