Nhằm giúp bạn đọc hiểu hơn về khối nón cũng như cách tính thể tích khối nón tiêu chuẩn, Invert xin chia sẻ đến bạn đọc một số thông tin liên quan đến khái niệm và công thức tính thể tích khối nón tiêu chuẩn dưới đây!
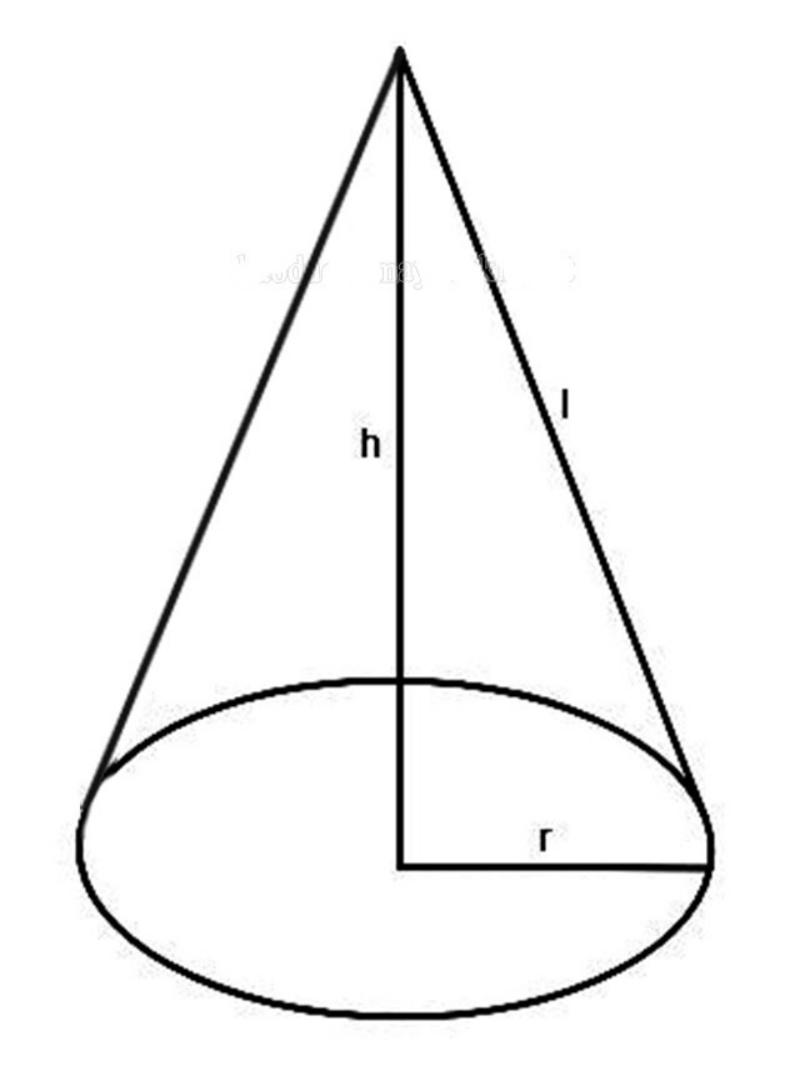
Hình nón là một hình khối không gian ba chiều có mặt đáy là hình tròn và một đỉnh duy nhất. Chúng ta có thể thể tưởng tượng hình nón là một hình chóp có đáy là hình tròn.
Các khái niệm liên quan đến khối nón
Để có thể tính được thể tích khối nón, bạn đọc sẽ cần tìm hiểu về một số khái niệm liên quan đến khối nón để có cái nhìn tổng quan nhất, từ đó dễ dàng xác định được các chỉ số và tính khối nón chuẩn.
Hình nón là một hình khối không gian ba chiều có mặt đáy là hình tròn và một đỉnh duy nhất. Có thể hiểu đơn giản hình nón là một hình chóp có đáy là hình tròn.
Các loại hình nón phổ biến hiện nay:
- Hình nón đều: Nếu hình chiếu của đỉnh xuống mặt đáy của hình nón trùng với tâm của mặt đáy, ta gọi đó là “hình nón đều”.
- Hình nón Xiên: Là hình nón có đỉnh không kéo vuông góc với tâm hình tròn mà có thể kéo từ 1 điểm bất kỳ mà không phải tâm của hình tròn mặt đáy. Ngược lại ta gọi đó là “hình nón xiên”. Tuy nhiên công thức tính thể tích của cả hai dạng hình nón này là giống nhau.
- Hình nón tròn xoay: Là hình nón có đỉnh nối vuông góc với mặt đáy tâm hình tròn.
- Hình nón cụt: Là hình nón có 2 hình tròn song song nhau.
Đường sinh của hình nón: Đường sinh bằng khoảng cách từ một điểm bất kỳ trên đường tròn đáy đến đỉnh của hình nón.
1. Mặt nón tròn xoay là gì?
Mặt nón hay được biết đến là mặt nón tròn xoay chính là mặt phẳng tạo thành một hình trong không gian thông qua mặt phẳng P chứa một đường thẳng d bất kỳ cùng với đường cong C. Lúc này, chúng ta sẽ cần quay mặt phẳng P quanh đường thẳng d với một góc 360. Đường cong C được tạo thành này sẽ được hiểu là mặt tròn xoay.
2. Hình nón hay khối nón là gì?
Để hiểu hình nón là gì, chúng ta sẽ cần tham khảo thông qua công thức cụ thể. Chẳng hạn, nếu chúng ta có mặt nón N với một trục tam giác có đỉnh là O, góc ở đỉnh này được xác định là 2α. Lúc này, P sẽ là một mặt phẳng vuông góc với tam giác đã cho tại điểm I khác với đỉnh O. Q ở đây sẽ được hiểu là mặt phẳng kết nối vuông góc với tam giác tại điểm O. P sẽ cắt N theo đường tròn có tâm là điểm I ( tạm gọi đường tròn này là T). Như vậy, phần của mặt nón được giới hạn bởi hai mặt phẳng là (P), (Q) cùng với hình tròn (T) sẽ được gọi là hình nón.
Hình nón kết hợp với phần bên trong của hình sẽ được gọi là khối nón. Có thể nói, hình nón sẽ được quy định bởi một mặt phẳng còn khối nón là khối hình trong không gian. Chẳng hạn khối hình của chiếc nón sẽ được gọi là kích thước của một khối nón thực tế.
Trong đó, hình tròn (T) lúc này sẽ được hiểu là đáy của hình nón, điểm O chính là đỉnh của hình nón đó với khoảng cách từ O đến mặt phẳng P được gọi là chiều cao của hình nón.
Nếu như M là một điểm bất kỳ nào đó trên mặt phẳng P thì lúc này đường OM sẽ được hiểu là đường sinh của hình nón đó. Đây chính là những yếu tố cơ bản cấu thành một hình nón hoàn chỉnh và hỗ trợ trong quá trình tính thể tích của hình nón hoặc bổ sung hỗ trợ cho nhau tính giá trị còn lại nếu không thể đo trực tiếp.
Công thức tính thể tích khối nón đơn giản
1. Công thức tính thể tích khối nón
Để tính được thể tích hình nón chúng ta có công thức tính thể tích khối nón như sau: Thể tích khối nón tính bằng 1/3 giá trị Pi nhân với bình phương bán kính đáy mặt nón và nhân chiều cao của hình nón.
Trong đó:
- V là thể tích của một hình nón bất kỳ
- R là bán kính mặt đáy
- H là đường cao hình nón
- π = 3,14
Lưu ý: Đơn vị đo khi tính thể tích là m3 (mét khối)
2. Công thức tính thể tích khối nón tròn xoay
Công thức tính thể tích của một khối nón tròn xoay là:
Trong đó:
- V là thể tích của khối nón tròn xoay.
- π là số Pi, có giá trị khoảng 3.14159.
- R là bán kính đáy của khối nón tròn xoay.
- h là chiều cao của khối nón tròn xoay.
- B là diện tích đáy
Lưu ý rằng trong công thức này, R và H phải được đo bằng cùng một đơn vị đo (ví dụ: cm, m, inch) để kết quả thể tích có cùng đơn vị với đơn vị của R và H.
3. Công thức tính thể tích khối nón cụt
Công thức tính thể tích của một khối nón cụt là:
Trong đó:
- V: Thể tích hình nón cụt
- r1, r2: Bán kính 2 đáy
- h: Chiều cao

4. Công thức tính diện tích xung quanh khối nón
Công thức diện tích xung quanh hình nón được tính theo công thức sau:
Trong đó:
- Sxq: Diện tích xung quanh
- r: Bán kính đáy
- l: Độ dài đường sinh
5. Công thức tính diện tích toàn phần hình nón
Diện tích toàn phần hình nón bằng diện tích xung quanh hình nón công với diện tích mặt đáy hình nón.
Trong đó:
- Stp: là diện tích toàn phần hình nón.
- π: là hằng số Pi = 3,14.
- l: đường sinh.
- r: Bán kính vòng tròn.
Cách xác định đường cao, bán kính đáy, đường sinh của hình nón
Đường cao h là khoảng cách từ tâm mặt đáy đến đỉnh hình chóp.
Đường sinh l là khoảng cách từ 1 điểm bất kỳ trên đường tròn đáy đến đỉnh hình chóp.
Do hình nón được tạo thành khi quay một tam giác vuông quanh trục một cạnh góc vuông của nó nên có thể bán kính đáy và đường cao là 2 cạnh góc vuông của tam giác, đường sinh là cạnh huyền. Nên khi biết đường cao h và bán kính đáy, ta tính được đường sinh bằng công thức như sau:
Biết bán kính và đường sinh, ta tính đường cao:
Khi biết đường cao và đường sinh, ta tính bán kính đáy theo công thức sau:
Hướng dẫn cách tính thể tích khối nón chi tiết
1. Cách tính diện tích mặt đáy của hình nón
- Với ví dụ đưa ra trong hình 1, bán kính mặt đáy của hình nón là 3 inches. Thay giá trị này vào công thức, ta có: A = π32.
- 32 = 3 *3, hay 9, vậy A = 9π.
- A = 28.27 in2
2. Cách tìm chiều cao của hình nón
3. Nhân diện tích mặt đáy với chiều cao của hình nón
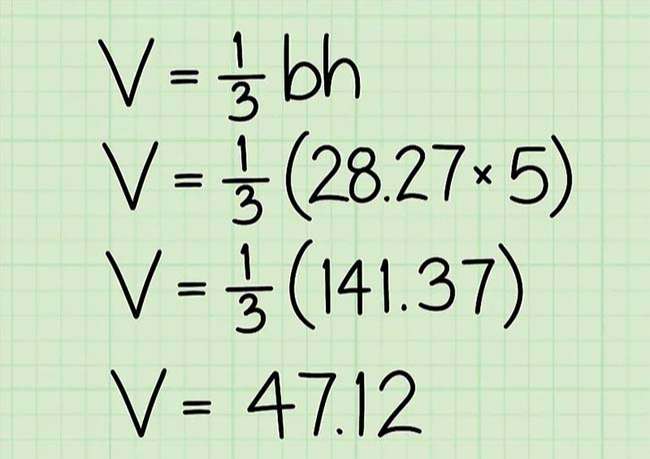
- Vậy Thể tích của hình nón là 141,35 * 1/3 = 47,12.
- Rút gọn các bước tính lại và được 1/3π325 = 47,12
Quy trình tính thể tích khối nón nhanh chóng
Nếu có sẵn các giá trị như bán kính và đường cao thì chúng ta chỉ việc áp dụng công thức và tính thể tích khối nón nhanh chóng. Tuy nhiên, nếu không có sẵn giá trị thì bạn cần tìm hiểu các bước để tính thể tích khối nón dưới đây!
1. Tính bán kính khối nón
Bán kính là một giá trị cơ bản nhất để tính được thể tích của hình nón. Vì vậy, nếu đề bài không cho sẵn bán kính thì bạn bắt buộc phải tìm giá trị này. Chẳng hạn:
- Nếu đề bài cho đường kính là d thì sẽ tính bán kính theo công thức d:2
- Nếu đề bài cho chu vi của hình tròn đáy thì chúng ta sẽ tìm bán kính bằng cách lấy giá trị chu vi : 2π.
- Nếu đề bài không cho các dữ kiện trên thì bạn cần trực tiếp lấy thước để đo khoảng cách lớn nhất của 3 điểm trên hình tròn đáy để lấy giá trị đường kính thực và chia cho 2, chúng ta sẽ có được bán kính chuẩn theo hình đã cho.
2. Tính diện tích đáy của khối nón
Để tính diện tích đáy của khối nón, bạn có thể áp dụng theo công thức S = π.r2 nếu đã biết bán kính r của hình nón. Nếu như chưa biết bán kính r, chúng ta cần quay lại bước 1 để tiến hành tính bán kính theo công thức đã cho.
3. Tính chiều cao của hình nón
Nếu như đề bài cho sẵn chiều cao, bạn chỉ cần áp dụng công thức tính khối nón đã cho trước đó. Tuy nhiên, nếu đề bài chưa so sẵn chiều cao thì bạn hãy tính như sau:
- Trong trường hợp biết đường sinh là l và bán kính r thì chúng ta sẽ tính chiều cao theo định lý Py-ta-go của tam giác vuông.
- Nếu như không cho sẵn các giá trị thì chúng ta sẽ cần đo trực tiếp giá trị bằng thước.
Khi đã biết được tất cả các đại lượng cơ bản thì bạn chỉ cần áp dụng công thức tính thể tích khối nón là V = 1/3.π.r2.h để tìm ra kết quả cuối cùng.
Một số bài tập thể tích khối nón
1. Bài tập tính thể tích khối nón có lời giải
Bài 1: Cho hình nón có đường sinh l, góc tạo bởi đường sinh và mặt phẳng đáy là 30º. Tính diện tích xung quanh của hình nón đó.
Giải: Để tính diện tích xung quanh của hình nón, ta cần tính độ dài quanh viền và chiều cao của nón.
Với góc giữa đường sinh và mặt phẳng đáy là 30º, ta có thể sử dụng công thức sử dụng hình tam giác:
h = l * sin(30º)
Sau đó, diện tích xung quanh của hình nón là tổng của diện tích mặt trên và diện tích quanh viền:
A = 2 * π * l * h + 2 * π * (l/2)^2
Trong đó, (l/2)^2 là diện tích mặt trên của hình nón.
Bài 2: Cho hình nón có chiều cao là 3a, bán kính đáy là 4a. Tính đường sinh, diện tích xung quanh, diện tích toàn phần và thể tích của hình nón trên.
Giải: Đường sinh của hình nón là đường nối tâm đáy đến trục cao nhất của hình nón. Đường sinh của hình nón có chiều dài là √(4a^2 + 3a^2) = √(25a^2).
Diện tích xung quanh: Diện tích xung quanh hình nón là tổng của diện tích của một vòng tròn và một hình tròn. Diện tích xung quanh của hình nón là A = 2πr (r = 4a) + πr^2 = 2π(4a) + π(4a^2) = 28πa^2.
Diện tích toàn phần: Diện tích toàn phần của hình nón là tổng của diện tích của một vòng tròn và một hình trụ. Diện tích toàn phần của hình nón là πr^2 + πr^2h = π(4a^2) + π(4a^2)(3a) = 52πa^2.
Thể tích: Thể tích của hình nón là V = (1/3)πr^2h = (1/3)π(4a^2)(3a) = 16π
Bài 3: Cho một hình tam giác ABC vuông cân tại A có cạnh AB = 2a. Quay tam giác này xung quanh cạnh AB tạo thành hình nón. Tính thể tích của khối nón được tạo thành.
Giải: Khi quay tam giác ABC xung quanh cạnh AB, sẽ tạo thành một khối nón với đường sinh là cạnh AB = 2a.
Chiều cao của khối nón là chiều cao của tam giác ABC từ đỉnh A, có thể tính bằng h = √(a^2 – (a/2)^2) = a√(3)/2.
Thể tích của khối nón là tổng của diện tích xung quanh và diện tích mặt trên:
V = π * (2a)^2 * h/3 + π * (2a/2)^2 * h/2
= 2π * a^2 * h/3
= 4π * a^3 / (3√3)
Bài 4: Một khối nón có thể tích bằng 30 π, nếu tăng bán kính khối nón đó lên 2 lần và giữ nguyên chiều cao thì thể tích của khối nón mới bằng bao nhiêu?
Giải: Giả sử chiều cao của khối nón ban đầu là h và bán kính của đáy là r. Thì thể tích của khối nón ban đầu là:
V = π * r^2 * h
Khi tăng bán kính của khối nón lên 2 lần, bán kính mới sẽ là 2r và thể tích mới sẽ là:
V’ = π * (2r)^2 * h = 4 * π * r^2 * h = 4 * V
Do thể tích ban đầu bằng 30π nên thể tích mới bằng 4 * 30π = 120π.
Bài 5: Cho thể tích khối nón bằng 4π vfa chiều cao là 3. Tính bán kính đường tròn đáy của khối nón
Giải: Thể tích của khối nón là 4π, chiều cao của nón là 3, vậy diện tích của đáy của nón là:
S = 4π / 3 = 4π / (1/3 * chiều cao)
Chúng ta có thể tìm ra bán kính đường tròn đáy của khối nón bằng cách sử dụng công thức diện tích hình tròn:
S = π * r^2
Vậy, chúng ta có thể tìm ra bán kính đường tròn đáy của khối nón bằng cách so sánh hai công thức trên:
π * r^2 = 4π / (1/3 * 3)
r^2 = 4 / (π * (1/3 * 3))
r = √(4 / (π * (1/3 * 3))) = √(4 / (π * 1)) = √(4 / π)
Vậy, bán kính đường tròn đáy của khối nón là √(4 / π).
Bài 6: Tính thể tích của khối nón biết thiết diện qua trục của nó là tam giác vuông cân. Tam giác này có cạnh huyền bằng 2a.
Giải: Thể tích của khối nón có thể tính bằng diện tích của một mặt cắt qua trục của nón, chia cho 2.
Diện tích mặt cắt qua trục của nón là diện tích của tam giác vuông cân tại trục của nón. Do đó, diện tích mặt cắt qua trục của nón là:
S = a^2 * √(3)/2
Vậy, thể tích của khối nón là:
V = S * 2a / 2 = a^3 * √(3)
Vậy, thể tích của khối nón biết thiết diện qua trục của nó là tam giác vuông cân có cạnh huyền bằng 2a là a^3 * √(3).
Bài 7: Tính thể tích khối nón có nón có chiều cao bằng 4 và đường sinh bằng 5
Giải: Thể tích của khối nón có chiều cao bằng 4 và đường sinh bằng 5 là:
V = π * (5/2)^2 * 4 / 3 = 10π
Vậy, thể tích của khối nón có chiều cao bằng 4 và đường sinh bằng 5 là 10π.
2. Bài tập tính thể tích khối nón không có lời giải
Bài 1: Cho khối nón có độ dài đường sinh bằng 5cm, bán kính hình tròn đáy là 3cm. Tính thể tích khối nón. Với l = 5 cm, R = 3 cm
Bài 2: Tính thể tích khối nón? Biết tứ diện đều ABCD có đỉnh A và có đường tròn đáy là đường tròn ngoại tiếp tam giác BCD và các cạnh bằng a.
Bài 3: Cho khối nón có đỉnh là O có độ dài đường sinh bằng 5 cm, bán kính hình tròn đáy là 3 cm. Tính thể tích khối nón, l = 5 cm R = 3 cm
Bài 4: Hãy tính thể tích khối nón khi cho hình nón N có góc ở đỉnh bằng 60 độ, mặt phẳng qua trục của hình nón, cắt hình nón theo một thiết diện là tam giác có bán kính đường tròn ngoại tiếp tam giác bằng 2.
Bài 5: Thể tích của khối nón có đường sinh bằng 10 và bán kính đáy bằng 6 là bao nhiêu?
Bài 6: Cho ABC vuông tại A, AB = 8cm, BC = 10cm, Tính thể tích khối tròn xoay tạo thành khi cho đường gấp khúc.
a) ACB quay quanh AB.
b) ABC quay quanh AC.
Hy vọng với những chia sẻ trên, bạn đọc đã hiểu khối nón là gì và biết cách tính thể tích khối nón theo đúng công thức chuẩn và áp dụng được vào thực tế quá trình học tập hay làm việc của bản thân.
