Công thức tính thể tích khối tứ diện là gì? Các bài tập áp dụng ra sao? Để giải đáp những thắc mắc này hãy cùng chúng tôi tìm hiểu thông tin trong nội dung dưới đây của bài viết.
Công thức tính thể tích khối tứ diện
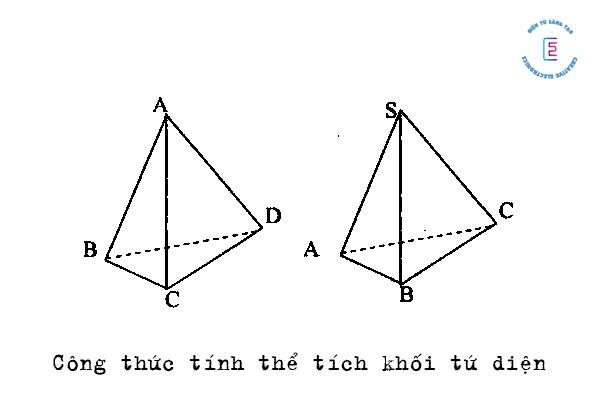
Kiến thức cần nắm vững:
Trong hình học thì tứ diện được biết là hình chóp tam giác với các khối đa diện gồm 4 mặt là tam giác, 6 cạnh thẳng và 4 góc đỉnh. Hình tứ diện được biết đến là một loại hình chóp với đa diện có đáy là tam giác phẳng và các mặt tam giác nối với đáy bằng 1 điểm chung. Do đó tứ diện cũng còn có thể được gọi là hình chóp tam giác.
Còn đối với tứ diện đều sẽ có 6 cạnh bằng nhau và 4 mặt sẽ là tam giác đều. Vậy nên trong tứ diện đều thì các mắt sẽ đều có cùng kích thước và hình dạng, tất cả các cạnh cũng vậy chúng đều có cùng 1 độ dài.
Công thức tính thể tích của khối tứ diện ABCD sẽ là như sau:
V = ⅓ SBCD . AH
(Thể tích tứ diện ABCD bằng 1 phần 3 diện tích mặt đáy nhân với chiều cao của khối tứ diện).
Công thức tính thể tích của khối tứ diện SABC sẽ là như sau:
V = ⅓ B . h
(Thể tích của khối chóp bằng 1 phần 3 nhân với diện tích mặt đáy và chiều cao của khối chóp).
Một số lưu ý bạn cần nắm vững:
- Trong quá trình tính toán các đại lượng, nếu cần cần thì bạn có thể đặt ẩn rồi tìm ra phương trình để giải ẩn đó
- Tứ diện hay hình chóp tam giác phải có 4 cách chọn đỉnh chóp.
- Với tứ diện nội tiếp hình hộp, tứ diện gần đều sẽ có 3 cặp cạnh đối bằng nhau nội tiếp hình hộp chữ nhất và tứ diện đều nội tiếp với hình lập phương.
- Để có thể tính được diện tích hoặc thể tích có khi ta cần phải tính gián tiếp bằng việc chia nhỏ các phần hoặc có thể lấy phần lớn hơn trừ đi các phần dư.
Các bài tập áp dụng công thức tính thể tích khối tứ diện
Bài tập 1: Cho tứ diện ABCD gần đều có các cặp cạnh đối bằng nhau AB = CD = a và AC = BD = b và AD = BC = c. Tính thể tích tứ diện ABCD.
Lời giải:
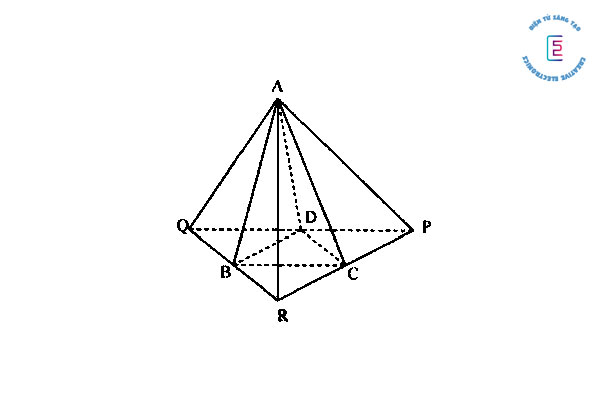

Bài tập 2: Cho tứ diện ABCD với các mặt ABC và ABD lần lượt là các tam giác đều cạnh a, các mặt ACD và BCD vuông góc với nhau.
- Tính thể tích khối tứ diện ABCD theo a.
- Tính số đo của góc giữa 2 đường thẳng AD và BC
Lời giải:
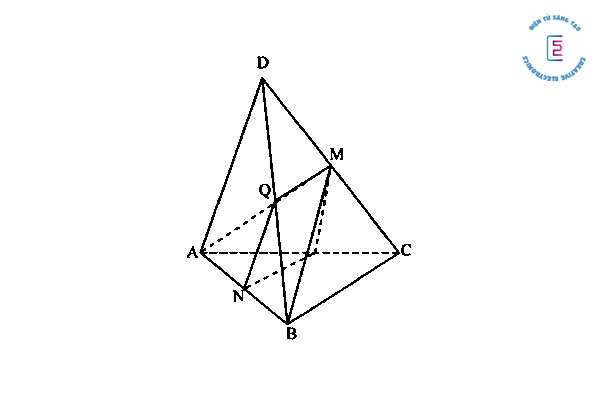

Bài tập 3: Cho tứ diện ABCD. Chứng minh thể tích tứ diện là không đổi trong các trường hợp:
- Đỉnh A di chuyển mặt phẳng (P) song song với BCD.
- Đỉnh A di chuyển trên đường thẳng d song song với BC.
- Hai đỉnh B và C di chuyển trên đường thẳng △ nhưng vẫn giữ nguyên độ dài.
Lời giải:
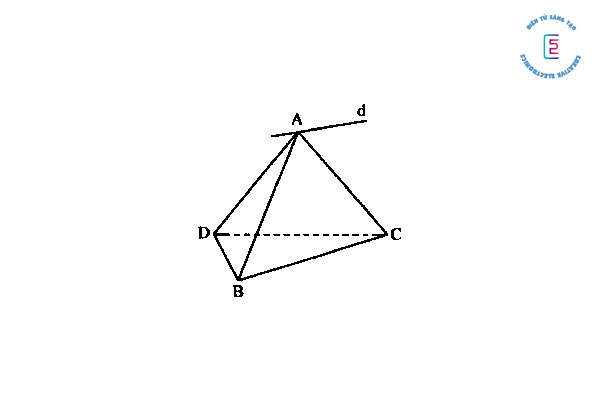
Thể tích tứ diện ABCD không đổi vì:
- a) Tam giác đáy BCD cố định và đường cao không đổi là khoảng cách từ A đến mặt phẳng (BCD), chính là khoảng cách giữa 2 mặt phẳng song song (P) và (BCD)
- b) Tam giác đáy BCD cố định và đường cao không đổi là khoảng cách từ A đến mặt phẳng (BCD), chính là khoảng cách giữa đường thẳng d với mặt phẳng song song (BCD).
- c) Đỉnh A và D cố định, diện tích đáy BCD là S = ½ BC. d(D, △) không đổi và chiều cao h = d(A, (D, △)) không đổi.
Bài tập 4: Cho tứ diện ABCD, gọi d là khoảng cách giữa 2 đường thẳng AB, CD, ∝ là góc giữa 2 đường thẳng đó. Chứng minh rằng VABCD = ⅙ AB . CD . d . sin∝.
Lời giải:
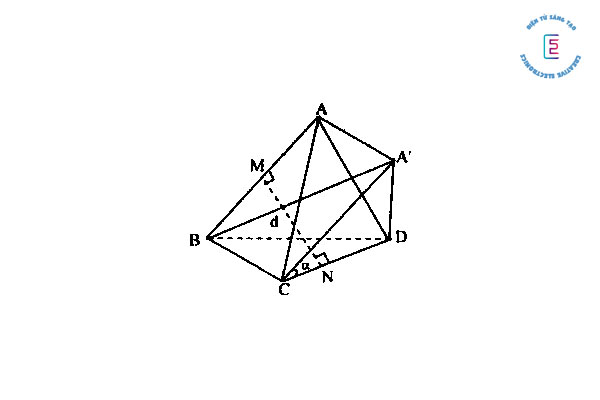

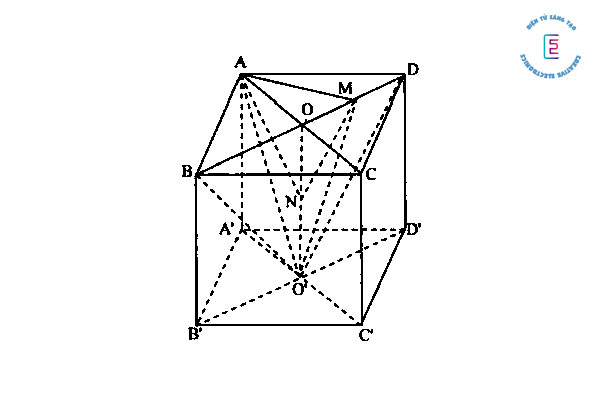
Bài tập 5: Cho hình lập phương ABCD. A’B’C’D’ có cạnh bằng a. Gọi O’ là tâm của mặt đáy A’B’C’D’ và điểm M nằm trên đường thẳng BD sao cho BM = ¾ BD. Tính thể tích khối tứ diện ABMO’ và khoảng cách giữa 2 đường thẳng AM và O’D.
Lời giải:

Trên đây là nội dung về công thức tính thể tích khối tứ diện và những bài tập áp dụng mà bạn có thể tham khảo. Hy vọng, với những thông tin trên sẽ giúp ích cho bạn trong quá trình học tập. Mọi thắc mắc hãy để lại thông tin cho chúng tôi dưới phần bình luận.