Các hàm lượng giác liên hệ các góc của một tam giác với độ dài các cạnh của nó. Các hàm lượng giác rất quan trọng trong việc nghiên cứu các hiện tượng tuần hoàn như sóng âm thanh và ánh sáng và nhiều ứng dụng khác. Ba tỉ số lượng giác quen thuộc nhất là hàm số sin , hàm số côsin và hàm số tiếp tuyến. Đối với góc nhỏ hơn góc vuông, hàm lượng giác thường được định nghĩa là tỷ số hai cạnh của tam giác vuông chứa góc và giá trị của chúng có thể được tìm thấy theo độ dài của các đoạn thẳng khác nhau xung quanh một đường tròn đơn vị.
Các góc được tính đối với các hàm sin, cos và tan là các hàm chính, trong khi các hàm cosecant, secant và cot được suy ra từ các hàm chính. Thông thường, các độ được coi là 0 °, 30 °, 45 °, 60 °, 90 °, 180 °, 270 ° và 360 °. Ở đây, bạn sẽ tìm hiểu giá trị của sin 90 độ và cách các giá trị được suy ra cùng với các giá trị độ hoặc radian khác.
Các mặt của một tam giác là gì? Xem xong 5 phút hiểu luôn.
Giá trị sin 90 độ
Để xác định hàm sin của một góc nhọn, hãy bắt đầu với tam giác vuông ABC với góc quan tâm và các cạnh của tam giác. Ba cạnh của tam giác được cho như sau:
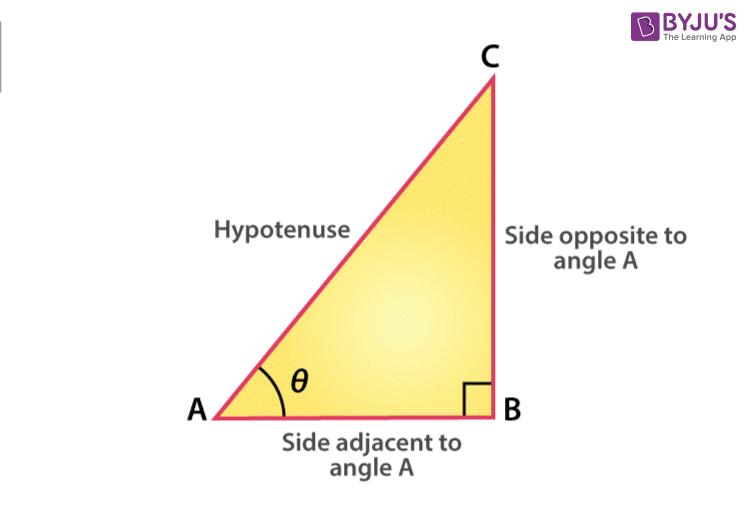
- Mặt đối diện – mặt đối diện với góc quan tâm.
- Cạnh huyền – cạnh đối diện của góc vuông và nó luôn là cạnh dài nhất của tam giác vuông
- Cạnh bên – cạnh còn lại của một tam giác và nó tạo thành một cạnh của cả góc ưa thích và góc vuông
Hàm sin của một góc bằng độ dài cạnh đối diện chia cho độ dài cạnh huyền và công thức được cho bởi
không cóθ =o p p o s i t e s i deh yp o t e n u s e s i deĐịnh luật sin phát biểu rằng các cạnh của một tam giác tỷ lệ với sin của các góc đối diện.
akhông cóA=bkhông cóB=ckhông cóCTrong các trường hợp sau, quy tắc sin được sử dụng. Những điều kiện đó là
Trường hợp 1: Cho hai góc và một cạnh (AAS và ASA)
Trường hợp 2: Cho hai cạnh và góc không bao gồm (SSA)
Động lực để tìm ra giá trị của tội lỗi 90 độ
Bây giờ chúng ta hãy tính giá trị của sin 90 °. Xét vòng tròn đơn vị. Đó là đường tròn có bán kính 1 đơn vị và tâm của nó được đặt tại gốc tọa độ.

Từ kiến thức cơ bản về lượng giác, chúng ta kết luận rằng đối với tam giác vuông đã cho, đơn vị đo cơ sở là ‘x’ và đơn vị đo vuông góc là ‘y’.
Chúng ta biết rằng,
Đối với tam giác vuông có số đo góc bất kỳ, hàm số sin bằng tỉ số giữa độ dài cạnh đối diện với độ dài cạnh huyền. Vì vậy, từ hình
không cóθ = và / 1
Bắt đầu đo các góc từ góc phần tư đầu tiên và kết thúc bằng 90 ° khi nó đạt đến trục y dương. Bây giờ giá trị của y trở thành 1 vì nó chạm vào chu vi của hình tròn. Do đó giá trị của y trở thành 1.
không cóθ = y / 1 = 1/1
Do đó, sin 90 độ bằng với giá trị phân số của 1/1.
Không có 90 ° = 1
Các hàm sin lượng giác phổ biến nhất là
- Sin 90 độ cộng với theta
không có(90∘+ θ ) = cosθ
- Sin 90 độ trừ theta
không có(90∘- θ ) = cosθMột số nhận dạng sin lượng giác khác như sau:
- không cóx =1cscx
- không có2x +cos2x = 1
- không có( – x ) = – sinx
- Sin 2x = 2 sin x cos x
Theo cách tương tự, chúng ta có thể suy ra các giá trị khác của góc sin như 0 °, 30 °, 45 °, 60 °, 90 °, 180 °, 270 ° và 360 °. Dưới đây là bảng lượng giác, xác định tất cả các giá trị của sin cùng với các tỷ số lượng giác khác.
Cos 0 độ
Giá trị của cos 0 độ bằng giá trị của sin 90 độ.
Sin 90 ° = Cos 0 ° = 1
Các ví dụ đã giải quyết
Câu 1: Tìm giá trị của sin 135 °.
Giải pháp:
Cho trước, sin 135 ° = sin (90 ° + 45 °)
= cos 45 ° [Kể từ khi không có(90∘+ θ ) =cosθ]
= 1 / √2
Do đó, giá trị của sin 135 ° là 1 / √2
Câu 2: Tìm giá trị của cos 30 °.
Giải pháp:
Cho trước, cos 30 ° = cos (90 ° – 60 °)
= Tội lỗi 60 ° [Kể từ khi cos(90∘- θ ) =không cóθ]
= 3√2
Do đó, giá trị của cos 30 ° là3√2.
Câu hỏi thực hành
- Đánh giá giá trị của sin 90 ° + Cos 90 °.
- Tìm giá trị của 2 giây 90 ° – giây 90 °
- Giá trị của (sin 90 °) / 2 – sin 30 ° là bao nhiêu?
