Làm thế nào để bạn biết nếu hai vectơ là các vectơ bằng nhau ? Có đủ độ lớn để chúng có cùng độ lớn hoặc cùng phương không? Trong trực tế:
“Hai hoặc nhiều vectơ được cho là bằng nhau nếu chúng có cùng độ dài hoặc độ lớn và chúng hướng theo cùng một hướng.”
Trong chủ đề này, chúng ta sẽ thảo luận về các khía cạnh sau của các vectơ bằng nhau:
- Khi nào hai vectơ bằng nhau?
- Làm thế nào để so sánh hai vectơ
Khi nào hai vectơ bằng nhau?
Hai hoặc nhiều vectơ bằng nhau khi chúng có cùng độ dài và cùng hướng. Hai hoặc nhiều vectơ bất kỳ sẽ bằng nhau nếu chúng thẳng hàng, được điều hướng và có cùng độ lớn.
Về mặt toán học, chúng ta có thể nói rằng hai vectơ A và B bằng nhau nếu chúng thỏa mãn các điều kiện sau:×
A = B (Vectơ A và B bằng nhau)
Nếu và chỉ nếu
| A | = | B | (Độ lớn bằng nhau)
và
A ↑ NO3 B (Cùng hướng)
Nếu hai vectơ bằng nhau thì vectơ cột của chúng cũng sẽ bằng nhau. Nói cách khác, hai hoặc nhiều vectơ bằng nhau nếu tọa độ của chúng bằng nhau.
Ví dụ , hãy xem xét các vectơ A = (ax1, ay1) và B = (bx1, by1). Nếu hai vectơ này bằng nhau thì:
ax1 = bx1 và ay1 = by1.
Các vectơ bằng nhau có thể có điểm bắt đầu và điểm kết thúc khác nhau, nhưng độ lớn và hướng của chúng phải giống nhau.
Ví dụ , tất cả các vectơ ngoại trừ AB trong hình dưới đây đều bằng nhau mặc dù chúng không trùng nhau. AB khác vật vì tuy có cùng độ lớn với các vật khác nhưng không cùng phương.
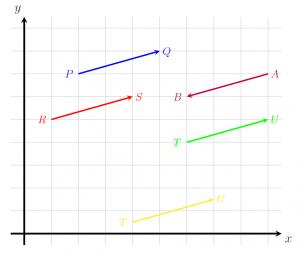
Làm thế nào để so sánh hai vectơ?
So sánh giữa các vectơ thực chất là so sánh độ lớn và hướng của các vectơ.
Phần này trước tiên sẽ so sánh các vectơ trong ba ví dụ khác nhau để tìm hiểu thêm về đẳng thức vectơ. Sau đó, chúng ta sẽ thảo luận về một số vấn đề thực hành và các giải pháp từng bước của chúng để phát triển sự hiểu biết sâu sắc hơn về chủ đề này.
Các ví dụ
ví dụ 1
Hãy xem xét hình ảnh được đưa ra dưới đây. So sánh hai vectơ a và b để xác định xem chúng có bằng nhau hay không.
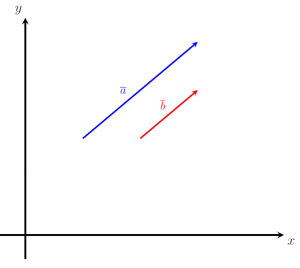
Giải pháp
Theo định nghĩa, hai vectơ bằng nhau nếu và chỉ khi chúng có cùng độ lớn và cùng hướng. Qua hình vẽ có thể thấy rằng vectơ a và vectơ b song song và hướng cùng phương nhưng độ lớn của chúng không bằng nhau. Như vậy, chúng ta có thể kết luận rằng các vectơ đã cho là không bằng nhau.
a ≠ b
Điều này tương đương với việc nói rằng một vectơ có độ dài 5m không thể bằng một vectơ có độ dài 10m. Hai đại lượng có độ lớn khác nhau không thể bằng nhau. Quy tắc tương tự áp dụng cho các đại lượng vô hướng.
Ví dụ 2
Hãy xem xét hình ảnh được đưa ra dưới đây. So sánh hai vectơ a và b để xác định xem chúng có bằng nhau hay không.
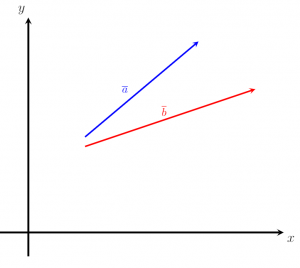
Giải pháp
Theo định nghĩa, hai vectơ bằng nhau nếu và chỉ khi chúng có cùng độ lớn và cùng hướng. Ví dụ này phức tạp hơn một chút so với ví dụ đầu tiên. Qua hình trên có thể thấy vectơ a và vectơ b có cùng độ lớn, nhưng hai vectơ không cùng phương. Như vậy, một lần nữa, chúng ta có thể kết luận rằng các vectơ đã cho là không bằng nhau.
a ≠ b
Điều này tương đương với tình huống hai xe rời cùng một nơi cùng một lúc. Một chiếc có vận tốc 50 dặm / giờ và đang di chuyển theo hướng đông bắc. Ôtô kia đang đi với vận tốc 50 dặm / giờ về hướng Nam. Sau một giờ, cả hai chiếc xe sẽ đi 50 dặm, nhưng họ sẽ đến điểm đến khác nhau. Tương tự, vận tốc của vectơ a và b từ hình vẽ không thể bằng nhau. Tức là hai vectơ có cùng độ lớn và khác phương thì không thể bằng nhau.
Ví dụ 3
Hãy xem xét hình ảnh được đưa ra dưới đây. So sánh hai vectơ a và b để xác định xem chúng có bằng nhau hay không.
Giải pháp
Ví dụ này khá đơn giản. Từ hình trên có thể thấy vectơ a và vectơ b có cùng độ lớn. Hai vectơ cũng chỉ cùng phương. Do đó, hai vectơ bằng nhau.
a = b
Ba ví dụ này cho thấy rằng hai vectơ chỉ bằng nhau nếu chúng có cùng độ dài và cùng hướng.
Ví dụ 4
Xác định độ lớn của hai vectơ:
- OW,có điểm ban đầu là O = (2,5) và điểm cuối cùng là W = (5,2), và
- PQ,có điểm ban đầu là P = (-4, 2) và điểm cuối cùng là Q = (3,6).
Hai vectơ có bằng nhau hay không?
Giải pháp
Chúng ta có thể sử dụng công thức khoảng cách để xác định độ lớn của vectơ OW đã cho :
| OW | = √ (5-2) ^ 2 + (2-5) ^ 2
Việc đơn giản hóa mang lại cho chúng ta:
| OW | = √ (3) ^ 2 + (-3) ^ 2
| OW | = √ 9 + 9
| OW | = √ 18
| OW | = √ 2 * 9
| OW | = √ 2 * (3) ^ 2
| OW | = 3 √ 2 đơn vị.
Như vậy, độ lớn của véc tơ OW xấp xỉ 4,242 đơn vị.
Bây giờ, chúng ta xác định độ lớn của vectơ PQ đã cho :
| PQ | = √ (3 – (- 4)) ^ 2 + (6-2) ^ 2
Đơn giản hóa để có được:
| PQ | = √ (7) ^ 2 + (4) ^ 2
| PQ | = √ 49 + 16
| PQ | = √ 65 đơn vị.
Như vậy, độ lớn của vectơ PQ xấp xỉ 8,062 đơn vị. Hai vectơ này không bằng nhau vì độ lớn và hướng của chúng không giống nhau.
OW ≠ PQ
Ví dụ 5
Xác định vectơ nào bằng nhau: a = (1; 2), b = (1; 3), và c = (1; 2)
Giải pháp
Chúng tôi sẽ so sánh các vectơ đã cho để xác định độ lớn và hướng của chúng. Chúng tôi có thể sử dụng thông tin này để quyết định xem chúng có bằng nhau hay không.
Đầu tiên, chúng tôi xác định độ lớn của các vectơ đã cho:
Đối với vectơ a = (1; 2):
| a | = √1 ^ 2 + 2 ^ 2
| a | = √5
Đối với vectơ b = (1; 3):
| b | = √1 ^ 2 + 3 ^ 2
| b | = √1 + 9
| b | = √10
Tương tự, đối với vectơ c = (1; 2):
| c | = √1 ^ 2 + 2 ^ 2
| c | = √5
Rõ ràng là | a | = | c |, nhưng | a | ≠ | b | và | b | ≠ | c | Chỉ có độ lớn của các vectơ a và c là giống nhau.
Để so sánh các hướng, chúng ta có thể vẽ ba vectơ trên mặt phẳng tọa độ, như trong hình dưới đây. Có thể quan sát thấy rằng cả ba vectơ đều song song với nhau và các mũi tên ở cùng phía. Có nghĩa là, tất cả chúng đều hướng về cùng một hướng
a ↑ b b ↑ direction cùng phương
Vì vectơ a và c có cùng độ dài và hướng nên ta có thể kết luận rằng vectơ a và c là các vectơ bằng nhau. Tuy nhiên, vectơ b không bằng a hoặc c
a = c
a ≠ b
b ≠ c
Ví dụ 6
Xác định giá trị của x để hai vectơ A = (2, 10) và B = (2, 5x) bằng nhau.
Giải pháp
Chúng ta biết rằng các vectơ đã cho sẽ bằng nhau nếu độ lớn và hướng của chúng giống nhau. Chúng ta có thể tìm giá trị của x khi đó như sau:
A = B => (2, 10) = (2, 5x)
Vì hai vectơ bằng nhau nên giá trị x và giá trị y trong vectơ cột sẽ bằng nhau. Đó là:
2 = 2
Và
10 = 5x.
Bằng cách đơn giản hóa phương trình trên, chúng ta nhận được:
x = 2
Như vậy, khi x = 2 thì hai vectơ A và B bằng nhau.
Ví dụ 7
Xác định giá trị của n để hai vectơ A = (-5, 1, 3n) và B = (-5, 1, 9) bằng nhau.
Giải pháp
Chúng ta biết rằng các vectơ đã cho sẽ bằng nhau nếu độ lớn và hướng của chúng giống nhau. Chúng ta có thể tìm giá trị của x khi đó như sau:
A = B => (-5, 1, 3n) = (-5, 1, 9)
Giá trị x, y và z của các vectơ cột phải giống nhau nếu các vectơ đó bằng nhau. Đó là:
-5 = -5, 1 = 1 và 3n = 9
Bằng cách đơn giản hóa 3n = 9 cho chúng ta:
n = 3
Như vậy, khi n = 3 thì hai vectơ A và B bằng nhau.
Ví dụ 8
Nếu hai vectơ X = (2 – p, 6 – q) và Y = (p – 6, q + 2) bằng nhau, hãy xác định giá trị sau:
- Giá trị của p và q mà bằng nhau
- Độ lớn của vectơ X và vectơ Y
Giải pháp
- Vì hai vectơ bằng nhau nên ta có thể viết phương trình: X = Y => (2 – p, 6 – q) = (p – 6, q + 2)
Đặt các giá trị x và y bằng nhau cho chúng ta:
2-p = p – 6
6-q = q + 2
Bằng cách đơn giản hóa các phương trình trên, chúng ta nhận được:
2 – p – p + 6 = 0
2p = 8
p = 4
Và
6 – q – q – 2 = 0
2q = 4
q = 2
Như vậy, khi p = 4 và q = 2, hai vectơ X và Y sẽ bằng nhau.
- Độ lớn của các vectơ X= (-2, 4) và Y= (-2, 4) là:
| X | = √4 + 16
| X | = √20
và
| Y | = √4 + 16
| Y | = √20.
Câu hỏi thực hành
Xác định độ lớn và hướng của các vectơ đã cho. Sau đó, kiểm tra xem chúng có bằng nhau hay không.
- A = (-1, -2/3, 0) và V = (2,5,3)
- T = (0, 2, -1) và D = (3,2,5)
- V = (2,5,3) và D = (3, -2,5)
- F = (4,10), G = (5, 5) và H = (4, 10)
- Vectơ OA trong đó O = (-1,0, 3) và A = (5,2,0); Vectơ UV, trong đó U = (1, -2, 0) và V = (-2,2, 0).
- Xác định giá trị của n để hai vectơ A = (-2n, 3, 2) và B = (8, 3, 2) bằng nhau
Câu trả lời
- Độ lớn của vectơ A đã cho là | A | = √ 13/9 đơn vị. Độ lớn của vectơ V đã cho là | V | = √ 38 đơn vị. Do đó, độ lớn không bằng nhau. Hướng của chúng cũng khác nhau nên các vectơ đã cho không bằng nhau. A ≠ V
- Độ lớn của vectơ T là | T | = √ 5 đơn vị, và độ lớn của vectơ D là | D | = √ 38 đơn vị. Các vectơ đã cho không bằng nhau vì cả độ lớn và hướng của các vectơ đều khác nhau.
- Độ lớn của vectơ V đã cho là | V | = √ 38 đơn vị, và độ lớn của vectơ D là | Đ | = √ 38 đơn vị. Mặc dù hai vectơ có cùng độ lớn nhưng phương của chúng không giống nhau. Do đó hai vectơ không bằng nhau.
- Độ lớn của F là | F | = √ 116 đơn vị. Độ lớn của G là | G | = √ 50 đơn vị, và độ lớn của H là | H | = √ 116 đơn vị. Các vectơ F và H hướng cùng phương, nhưng vectơ G hướng khác hướng. Do đó, chỉ có các vectơ F và H là bằng nhau. Đó là, | F | = | H |, | F | ≠ | G |, | G | ≠ | H |, và F ↑.
Vì vậy,
F = H
- Độ lớn của vectơ OA là | OA | = 7 đơn vị, và độ lớn của vectơ UV là | UV | = 5 đơn vị. Rõ ràng, hai vectơ không bằng nhau vì độ lớn của chúng không bằng nhau.
- Bằng cách đặt các giá trị x tương ứng bằng nhau, ta thấy rằng khi n = -4 thì hai vectơ A và B sẽ bằng nhau.
Xem thêm:
Khám phá các thành phần Vector quan trọng nhất hiện nay
Vectơ 3D và những ví dụ cụ thể nhất
