Một tam giác có ba góc trong tương ứng với ba đỉnh của tam giác đó và các góc ngoài là các góc kề bù với các góc trong của tam giác đó. Và trong bài viết sau đây chúng ta sẽ cùng nhau tìm hiểu về góc ngoài của tam giác cũng như các dạng bài tập liên quan đến góc ngoài của tam giác.
I. Góc ngoài của tam giác là gì?
– Góc ngoài của một tam giác là góc kề bù với một góc trong của tam giác đó.
Chẳng hạn như ta có hình vẽ sau:
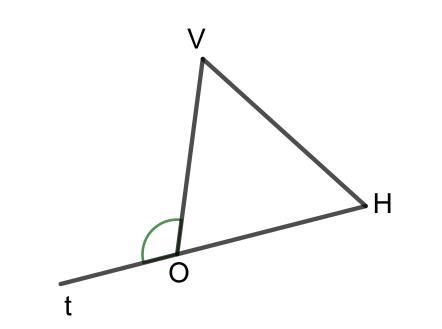
Quan sát hình vẽ trên ta thấy góc kề bù với góc trong của tam giác VOH nên chính là góc ngoài của tam giác VOH
II. Tính chất góc ngoài của tam giác
– Tính chất: Mỗi góc ngoài của tam giác bằng tổng hai góc trong không kề với nó.
Ta có thể dễ dàng chứng minh tính chất này như sau:

Chứng minh: Vì tổng ba góc của một tam giác bằng 180o nên ta có:
+ + = 180o
⇒ = 180o – ( + ) (1)
Mặt khác, ta lại có góc là góc ngoài của tam giác VOH mà theo khái niệm về góc ngoài của tam giác thì:
+ = 180o (hai góc kề bù)
⇒ = 180o – (2)
Từ (1) và (2) ta suy ra: = 180o – ( + ) = 180o –
Suy ra: = +
Từ đó ta có thể suy ra điều phải chứng minh.
III. Các dạng bài tập cơ bản về góc ngoài của tam giác
1. Dạng 1: Nhận biết góc ngoài của tam giác
*Phương pháp giải: Dựa vào khái niệm và tính chất của góc ngoài của tam giác
*Ví dụ: Trong các hình vẽ sau, hình vẽ nào thể hiện góc là góc ngoài của tam giác VOH?

Giải:
Quan sát các hình vẽ trên, ta thấy:
– Hình 1: là góc kề bù với góc nên là góc ngoài của tam giác VOH.
– Hình 2: là một góc bẹt, không kề bù với bất kì góc trong nào của tam giác VOH nên không phải là góc ngoài của tam giác VOH.
– Hình 3: là góc kề với góc nhưng + = 135o < 180o .
Suy ra: không kề bù với bất kì góc trong nào của tam giác VOH.
Vậy không phải là góc ngoài của tam giác VOH.
Kết luận: Trong các hình vẽ trên chỉ có hình 1 thể hiện góc là góc ngoài của tam giác VOH.
2. Dạng 2: Tính số đo các góc của tam giác
*Phương pháp giải: Dựa vào các kiến thức về tổng số đo 3 góc của một tam giác, góc ngoài của tam giác và các kiến thức về góc đã được học để tính số đo các góc của tam giác.
*Ví dụ: Cho ΔSOV là tam giác đều và là góc ngoài của tam giác SOV. Hãy tính số đo tất cả các góc có trong tam giác SOV và .
Giải:
Ta có hình vẽ sau:

Vì ΔSOV là tam giác đều nên ta có: = = = 60o
Mặt khác, vì là góc ngoài của tam giác SOV mà theo hình vẽ trên thì chính là góc
Từ đó ta có: = + = 60o + 60o = 120o
Vậy số đo các góc có trong tam giác SOV là:
= = = 60o , = 120o
IV. Một số bài tập vận dụng về góc ngoài của tam giác
Bài 1: Cho tam giác SHB.
a. Theo em, có nhiều nhất là bao nhiêu góc ngoài của tam giác SHB. Hãy thể hiện các góc ngoài đó trên hình vẽ.
b. Em có nhận xét gì về các góc ngoài của tam giác SHB vừa vẽ.
ĐÁP ÁN
Giải:
Theo em, có nhiều nhất là 6 góc ngoài của tam giác SHB .

b. Tương ứng với mỗi đỉnh của tam giác SHB ta sẽ có 2 góc ngoài và 2 góc này là hai góc đối đỉnh với nhau.
Bài 2: Cho tam giác BVP là tam giác đều. Vẽ tia Vx là tia đối của tia VB, tia Vy là tia đối của tia VP.
a. Góc có phải là góc ngoài của ΔBVP không? Vì sao?
b. Tính số đo các góc ngoài của ΔBVP tương ứng với đỉnh V bằng hai cách.
ĐÁP ÁN
Giải:
Ta có hình vẽ sau:

a. Góc không phải là góc ngoài của ΔBVP. Vì không kề bù với bất kì góc trong nào của ΔBVP.
b. Các góc ngoài của ΔBVP tương ứng với đỉnh V chính là góc và
Cách 1: Áp dụng khái niệm góc ngoài của tam giác.
Vì là góc ngoài của ΔBVP tương ứng với đỉnh V nên kề bù với
Từ đó, ta có: + = 180o (hai góc kề bù)
Mà = 60o (vì ΔBVP là tam giác đều)
Suy ra: = 180o – = 180o – 60o = 120o
Ta lại có, và là hai góc đối đỉnh nên = = 120o
Cách 2: Áp dụng tính chất của góc ngoài của tam giác.
Vì là góc ngoài của ΔBVP mà theo tính chất về góc ngoài của tam giác thì sẽ bằng tổng hai góc trong không kề với nó.
Có nghĩa là: = +
Mà = = 60o (Vì ΔBVP là tam giác đều)
Suy ra: = + = 60o + 60o = 120o
Ta lại có, và là hai góc đối đỉnh nên = = 120o
Vậy số đo hai góc ngoài của ΔBVP tương ứng với đỉnh V là: = = 120o
Bài 3: Xét sự đúng, sai của các phát biểu sau bằng cách đánh dấu Χ vào ô Đúng hoặc Sai.
Khẳng địnhĐúngSai1) Một tam giác có nhiều nhất là 3 góc ngoài tương ứng với 3 đỉnh của tam giác đó2) Mỗi góc ngoài của tam giác bằng tổng hai góc trong không kề với nó3) Mỗi góc ngoài của tam giác có số đo bằng góc trong kề bù với nó4) Tương ứng với mỗi đỉnh của một tam giác sẽ có hai góc ngoài có số đo bằng nhau5) Góc ngoài của một tam giác là góc kề bù với một góc trong của tam giác đóĐÁP ÁNKhẳng địnhĐúngSai1) Một tam giác có nhiều nhất là 3 góc ngoài tương ứng với 3 đỉnh của tam giác đóX2) Mỗi góc ngoài của tam giác bằng tổng hai góc trong không kề với nóX3) Mỗi góc ngoài của tam giác có số đo bằng góc trong không kề với nóX4) Tương ứng với mỗi đỉnh của một tam giác sẽ có hai góc ngoài có số đo bằng nhaux5) Góc ngoài của một tam giác là góc kề bù với một góc trong của tam giác đóx
Trên đây là toàn bộ kiến thức về góc ngoài của tam giác, các dạng bài tập cơ bản về góc ngoài của tam giác có phương pháp giải và ví dụ cụ thể cùng với một số bài tập vận dụng có lời giải chi tiết, dễ hiểu. Hy vọng những kiến thức trên sẽ giúp các bạn học sinh hiểu rõ hơn về góc ngoài của tam giác cũng như áp dụng vào giải các bài tập liên quan đến chủ đề này một cách nhanh gọn và chính xác nhất.
Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang
