1. Định nghĩa phương trình đường elip lớp 10
Trong mặt phẳng, cho hai điểm cố định F1 và F2. Elip là tập hợp các điểm M sao cho tổng $F_{1}M+F_{2}M=2a$ không đổi.
Trong đó các điểm $F_{1},F_{2}$ gọi là tiêu điểm của elip.
Khoảng cách $F_{1}F_{2}=2c$ gọi là tiêu cự của elip.
2. Phương trình chính tắc của đường elip
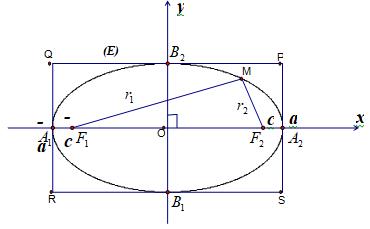
Cho elip có tiêu điểm $F_{1},F_{2}$ chọn hệ trục tọa độ Oxy sao cho $F_{1}(-c;0)$ và $F_{2}(c;0)$. Khi đó người ta chứng minh được:
$Mleft ( x;y right )epsilon$ elip $Rightarrow frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=1$ (1)
Trong đó: $b^{2}=a^{2}-c^{2}$
Phương trình (1) được gọi là phương trình chính tắc của đường elip.
Ví dụ: Trong mặt phẳng với hệ trục tọa độ Oxy, cho elip ( E) có độ dài trục lớn bằng 12 và độ dài trục bé bằng 6. Hãy viết phương trình chính tắc của elip (E)?
Giải:
Phương trình chính tắc của elip có dạng $frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=1$ (a,b > 0).
Ta có độ dài trục lớn bằng 12 nên 2a = 12 => a = 6
Ta có độ bé bằng 6 nên 2b = 6 => b = 3
Vậy phương trình của Elip là: $frac{x^{2}}{36}+frac{y^{2}}{9}=1$
Đăng ký ngay để nhận bộ tài liệu nắm trọn kiến thức và phương pháp giải mọi dạng bài tập Toán thi THPT Quốc gia

3. Thành phần và hình dạng của elip
Với elip (E) có phương trình (1):
Nếu điểm M(x;y) thuộc (E) thì các điểm $M_{1}$(-x;y), $M_{2}$=(x;-y) cũng thuộc (E).
Vậy (E) có:
+ Các trục đối xứng: Ox, Oy
+ Tâm đối xứng là gốc O

Thay y = 0 vào (1) ta có $x=pm a$, suy ra (E) cắt Ox tại hai điểm $A_{1}$=(-a;0) và $A_{2}=(a;0)$.
Tương tự thay x=0 vào (1) ta được y=b, vậy (E) cắt Oy tại hai điểm $B_{1}=(0;-a),B_{2}=(a;0)$.
Các điểm $A_{1},A_{2},B_{1},B_{2}$ gọi là các đỉnh của elip.
Trong đó đoạn thẳng $A_{1},A_{2}$ là trục lớn, đoạn thẳng $B_{1},B_{2}$ là trục nhỏ của elip.
Ví dụ: Xác định độ dài các trục, toạ độ các tiêu điểm, toạ độ các đỉnh và vẽ elip (E) có phương trình: $frac{x^{2}}{25}+frac{y^{2}}{9}=1$
Giải:
Vì phương trình đường elip có dạng $frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=1$
$left{begin{matrix}a^{2}=25 b^{2}=9end{matrix}right.$ $Leftrightarrow left{begin{matrix}a=5 b=3end{matrix}right.$
$c=sqrt{a^{2}-b^{2}}=4$
Vậy (E) có:
– Trục lớn : $A_{1}A_{2}$ = 2a =10
– Trục nhỏ : $B_{1}B_{2}$ = 2b = 6
– Hai tiêu điểm: $F_{1}$(- 4;0), $F_{2}$(4;0)
– Bốn đỉnh: $A_{1}$(- 5;0), $A_{2}$(5;0), $B_{1}$(0;- 3), $B_{2}$(0;3).
4. Các dạng bài tập về phương trình đường elip
Câu 1: Cho Elip (E): $frac{x^{2}}{16}+frac{y^{2}}{12}=1$ và điểm M nằm trên (E). Giả sử điểm M có hoành độ bằng 1 thì các khoảng cách từ M tới 2 tiêu điểm của (E) bằng bao nhiêu?
Giải:
Ta có $a^{2}=16,b^{2}=12$
nên $c^{2}=a^{2}-b^{2}=4$ $Rightarrow a=4;c=2$ và hai tiêu điểm $F_{1}$(-2; 0); $F_{2}$(2;0)
Điểm M thuộc (E) và $x_{M}=1Rightarrow y_{M}pm frac{3sqrt{5}}{2}$
Tâm sai của elip $e=frac{c}{a}Rightarrow e=frac{2}{4}=frac{1}{2}$ $Rightarrow MF_{1}=a+ex_{M}=4+0.5=4.5$ $MF_{2}=a-ex_{M}=4-0.5=3.5$
Câu 2: Trong mặt phẳng tọa độ Oxy, viết phương trình chính tắc của elip (E) có tâm sai bằng $frac{sqrt{3}}{3}$ và độ dài đường chéo hình chữ nhật cơ sở bằng $2sqrt{5}$.
Giải:
Gọi phương trình chính tắc của elip (E) có dạng: $frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}$ với a>b>0
Tâm sai $e=frac{c}{a}=frac{sqrt{3}}{3}Leftrightarrow c^{2}=frac{a^{2}}{sqrt{3}}$.
Độ dài đường chéo hình chữ nhật $sqrt{left ( 2a right )^{2}+left ( 2b right )^{2}}=2sqrt{5}Leftrightarrow a^{2}+b^{2}=5Leftrightarrow b^{2}=5-a^{2}$
Khi đó: $a^{2}=b^{2}+c^{2}Leftrightarrow a^{2}=5-a^{2}+frac{a^{2}}{3}Leftrightarrow a^{2}=3Rightarrow b^{2}=2$
Vậy phương trình chính tắc của elip (E) cần lập là: $frac{x^{2}}{3}+frac{y^{2}}{2}=1$
Đăng ký ngay để được các thầy cô ôn tập và xây dựng lộ trình ôn thi THPT sớm ngay từ bây giờ

Câu 3: Trong mặt phẳng tọa độ Oxy. Viết phương trình chính tắc của elip (E) biết rằng elip (E) có hai tiêu điểm $F_{1},F_{2}$, với $F_{1}(-sqrt{3};0)$ và có một điểm M thuộc (E) để tam giác F1MF2 vuông tại M và có S=1.
Giải:
Gọi phương trình chính tắc của elip (E) có dạng: $frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}$ với a>b>0
Với $F_{1}(-sqrt{3};0)$, suy ra $c=sqrt{3}$ => $a^{2}-b^{2}-c^{2}=3$ hay $a^{2}=b^{2}+3$ (1)
Gọi $Mleft ( x_{0};y_{0} right )$ $Rightarrowleft{begin{matrix} vec{MF_{1}}=left ( -sqrt{3}-x_{0};-y_{0}right ) vec{MF_{2}}=left ( sqrt{3} -x_{0};-y_{0}right )end{matrix}right.$
Khi đó: $widehat{F_{1}MF_{2}}=90^{circ}$ $Leftrightarrow overline{MF_{1}}.overline{MF_{2}}=0$ $Leftrightarrow x_{0}^{2}-3+y_{0}^{2}=0$ $Leftrightarrow x_{0}^{2}+y_{0}^{2}=3$
Ta có: $S_{F_{1}MF_{2}}=frac{1}{2}d(M,Ox).F_{1}F_{2}=frac{1}{2}left | y_{0} right |.2sqrt{3}=sqrt{3}left | y_{0} right |=1$ $Leftrightarrow y_{0}^{2}=frac{1}{3}$ $Rightarrow x_{0}^{2}=frac{8}{3}$
Mặt khác $M(x_{0};y_{0})epsilon (E)$ $Leftrightarrow frac{x_{0}^{2}}{a^{2}}+frac{y_{0}^{2}}{b^{2}}=1$ $Leftrightarrow frac{8}{3a^{2}}+frac{1}{3b^{2}}=1$ (2)
Thay (1) vào (2) ta được: $frac{8}{3(b^{2}+3)}+frac{1}{3b^{2}}=1Leftrightarrow 3b^{4}=3Leftrightarrow b=1$ (do b>0) $Rightarrow a^{2}=4$
Vậy phương trình chính tắc của elip (E) cần lập là: $frac{x^{2}}{4}+y^{2}=1$
Bài 4: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): $x^{2}+y^{2}=8$. Biết (E) có độ dài trục lớn bằng 8 và (E) cắt (C) tại bốn điểm tạo thành bốn đỉnh của một hình vuông. Hãy viết phương trình chính tắc elip (E).
Giải:

Ta có phương trình chính tắc của elip (E) có dạng: $frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=1$
– (E) có độ dài trục lớn bằng 8 nên suy ra 2a = 8 => a = 4.
– (E) cắt (C) tại 4 điểm phân biệt tạo thành 4 đỉnh của một hình vuông => 4 đỉnh nằm trên hai đường phân giác thuộc góc phần tư thứ nhất và thứ hai.
Ta giả sử A là một giao điểm của (E) và (C) thuộc đường phân giác Δ: y = x.
– Gọi $A(t;t)epsilon Delta $ (t > 0). Ta có: $Aepsilon(C)Rightarrow t^{2}+t^{2}=8Leftrightarrow t=2$ (vì t > 0) => A(2;2)
– Mà $Aepsilon(E)Rightarrow frac{2^{2}}{4^{2}}+frac{2^{2}}{b^{2}}=1Rightarrow b^{2}=frac{16}{3}$
Vậy phương trình chính tắc của elip (E) là: $frac{x^{2}}{16}+frac{y^{2}}{frac{16}{3}}=1$
Câu 5: Trong mặt phẳng tọa độ Oxy, cho elip (E) có hai tiêu điểm $F_{1}(-sqrt{3};0),F_{2}(sqrt{3};0)$ và đi qua điểm $A(sqrt{3};frac{1}{2})$. Hãy lập phương trình chính tắc của (E) và với mọi điểm M thuộc (E), hãy tính giá trị biểu thức: $P=MF_{1}^{2}+MF_{2}^{2}-3OM^{2}-MF_{1}MF_{2}$.
Giải:
– Gọi phương trình chính tắc của elip (E) có dạng: $frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=1$ với a>b>0
(E) có hai tiêu điểm $F_{1}(-sqrt{3};0),F_{2}left ( sqrt{3};0right )$ suy ra $c=sqrt{3}$
– Khi đó a² – b² = c² = 3 ⇔ a² = b² +3 => (E): $frac{x^{2}}{b^{2}+3}+frac{y^{2}}{b^{2}}=1$
– Với $Aleft ( sqrt{3};frac{1}{2}right )epsilon (E)$ ⇔ $frac{3}{b^{2}+3}+frac{1}{4b^{2}}=1$ ⇔ $4b^{2}-b^{2}-3=0Leftrightarrow left ( 4b^{2}+3right )left ( b^{2}-1 right )=0$ $Leftrightarrow b^{2}=1Rightarrow a^{2}=4$
Vậy phương trình chính tắc của (E) là: $frac{x^{2}}{4}+y^{2}=1$
$M(x_{0};y_{0})epsilon (E)Rightarrowleft{begin{matrix} MF_{1}=a+frac{c}{a}x_{0};MF_{2}=a-frac{c}{a}x_{0}OM^{2}=x_{0}^{2}+y_{0}^{2};frac{x_{0}^{2}}{4}+y_{0}^{2}=1end{matrix}right.$
Khi đó:
P = $left ( a+frac{c}{a}x_{0} right )^{2}+left ( a-frac{c}{a}x_{0} right )^{2}-3(x_{0}^{2}+y_{0}^{2})-(a+frac{c}{a}x_{0})(a-frac{c}{a}x_{0})$
= $x^{2}+frac{3c^{2}}{a^{2}}x_{0}^{2}-3(x_{0}^{2}+y_{0}^{2})$
= $4+frac{9}{4}x_{0}^{2}-3(x_{0}^{2}+y_{0}^{2})$
= $4-3(frac{x_{0}^{2}}{4}+y_{0}^{2})$
= 4-3=1
Vậy P = 1
Thông qua những kiến thức trong bài viết, hi vọng các em đã có thể vận dụng lý thuyết vào làm bài tập về phương trình đường elip. Để có thể học thêm nhiều phần bài giảng thú vị và chi tiết khác, các em có thể truy cập ngay Vuihoc.vn để đăng ký tài khoản để bắt đầu quá trình học tập của mình nhé!
