Đường trung trực là một trong những nội dung quan trọng sẽ được học trong chương trình hình học lớp 7. Vậy tính chất đường trung trực là gì? Các dạng bài tập đường trung trực như thế nào. Mời các bạn hãy cùng Download.vn theo dõi bài viết dưới đây nhé.
Đường trung trực tổng hợp kiến thức lý thuyết về khái niệm, tính chất kèm theo các dạng bài tập có đáp án và lời giải chi tiết. Đây là tài liệu hỗ trợ học sinh lớp 7 trong quá trình học tập, ôn luyện tại nhà được tốt hơn. Bên cạnh đó các em tham khảo thêm: cách chứng minh 3 điểm thẳng hàng, bài tập về lũy thừa số hữu tỉ, bài tập Nhân chia số hữu tỉ.
I. Đường trung trực là gì?
Đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng gọi là đường trung trực của đoạn thẳng ấy.

Định lý 1: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
GT: d là trung trực của AB, M ∈ d
=> KL: MA = MB
Định lí 2:
Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó
Nhận xét: Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.
II. Tính chất đường trung trực
2.1. Tính chất đường trung trực của một đoạn thẳng
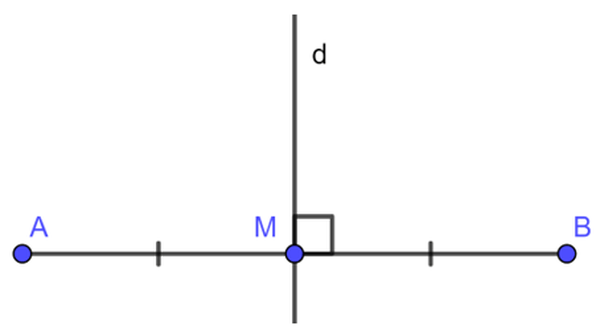
Trên hình vẽ trên, dd là đường trung trực của đoạn thẳng AB.AB. Ta cũng nói: AA đối xứng với BB qua d.d.
Nhận xét:
Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.
2.2. Tính chất ba đường trung trực của tam giác
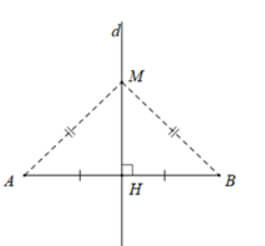
Trên hình, điểm OO là giao điểm các đường trung trực của ΔABC.ΔABC.
Ta có OA=OB=OC.OA=OB=OC. Điểm OO là tâm đường tròn ngoại tiếp ΔABC.ΔABC.
III. Các dạng toán thường gặp
Dạng 1: Chứng minh đường trung trực của một đoạn thẳng
– Phương pháp:
Để chúng minh dd là đường trung trực của đoạn thẳng ABAB, ta chứng minh dd chứa hai điểm cách đều AA và BB hoặc dùng định nghĩa đường trung trực.
Dạng 2: Chứng minh hai đoạn thẳng bằng nhau
– Phương pháp:
Ta sử dụng định lý: “Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.”
Dạng 3: Bài toán về giá trị nhỏ nhất
Phương pháp:
– Sử dụng tính chất đường trung trực để thay độ dài một đoạn thẳng thành độ dài một đoạn thẳng khác bằng nó.
– Sử dụng bất đẳng thức tam giác để tìm giá trị nhỏ nhất.
Dạng 4: Xác định tâm đường tròn ngoại tiếp tam giác
Phương pháp:
Sử dụng tính chất giao điểm các đường trung trực của tam giác
Định lý: Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.
Dạng 5: Bài toán liên quan đến đường trung trực đối với tam giác cân
Phương pháp:
Chú ý rằng trong tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung tuyến , đường phân giác ứng với cạnh đáy này.
Dạng 6: Bài toán liên quan đến đường trung trực đối với tam giác vuông
Phương pháp:
Ta chú ý rằng: Trong tam giác vuông, giao điểm các đường trung trực là trung điểm cạnh huyền
IV. Một số câu hỏi thường gặp về đường trung trực
Số đường trung trực trong một đoạn thẳng?
Vì đường trung trực là đường thẳng đi qua trung điểm và vuông góc với đoạn thẳng. Mà mỗi đoạn thẳng chỉ có duy nhất một điểm là trung điểm cho nên mỗi đoạn thẳng có duy nhất 1 đường trung trực.
Cách viết phương trình đường trung trực của đoạn thẳng
Khi tìm hiểu về định nghĩa đường trung trực của đoạn thẳng, ta cũng cần biết cách viết phương trình đường trung trực của đoạn thẳng như sau:
Bước 1. Ta tìm vectơ pháp tuyến của đường trung trực và một điểm mà nó đi qua.
Bước 2. Ta dựa vào định lý 1: “Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó. Nghĩa là nếu điểm M thuộc đường thẳng AB thì thì MA = MB.
Ví dụ 1: Gọi M là điểm nằm trên đường trung trực của đoạn thẳng AB. Nếu MA có độ dài 5cm thì độ dài MB bằng bao nhiêu?
Giải:
Vì điểm M nằm trên đường trung trực của đoạn thẳng AB nên theo định lí về tính chất của các điểm thuộc đường trung trực ta có MA = MB. Mà MA = 5cm (gt) suy ra MB = 5cm.
Ví dụ 2: Vẽ một đoạn thẳng MN, sau đó hãy dùng thước thẳng và compa để dựng đường trung trực của đoạn thẳng đó.
Ví dụ 3: Gọi M là điểm nằm trên đường trung trực của đoạn thẳng AB, cho đoạn thẳng MA có độ dài 5cm. Hỏi độ dài MB bằng bao nhiêu?
Ví dụ 3:
Chứng minh đường thẳng PQ được vẽ như trong hình 43 đúng là đường trung trực của đoạn thẳng MN.
Gợi ý: Sử dụng định lí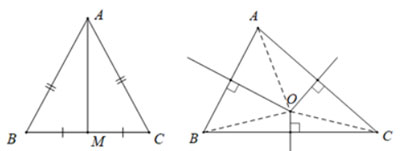
Giải:
Ta có : Hai cung tròn tâm M và N có bán kính bằng nhau và cắt nhau tại P, Q.
Nên MP = NP và MQ = NQ
⇒ P; Q cách đều hai mút M, N của đoạn thẳng MN
nên theo định lí 2 : P; Q thuộc đường trung trực của MN
hay đường thẳng qua P, Q là đường trung trực của MN.
Vậy PQ là đường trung trực của MN.
Ví dụ 4
Cho ba tam giác cân ABC, DBC, EBC có chung đáy BC. Chứng minh ba điểm A, D, E thẳng hàng.
Gợi ý đáp án
Bài 1: Cho tam giác ABC cân tại A. Hai trung tuyến BM, CN cắt nhau tại I. Hai tia phân giác trong của góc B và C cắt nhau tại O.Hai đường trung trực của 2 cạnh AB và AC cắt nhau tại K.
a) Chứng minh: BM = CN.
b) Chứng minh OB = OC
c) Chứng minh các điểm A,O, I, K thẳng hàng.
Bài 2: Trên đường thẳng d là trung trực của đoạn thẳng AB lấy điểm M, N nằm ở hai nữa hai mặt phẳng đối nhau có bờ là đường thẳng AB.
a) Chứng minh
b) MN là tia phân giác của AMB.
Bài 3: Cho góc xOy = 50, điểm A nằm trong góc xOy. Vẽ điềm M sao cho Ox là trung trực của đoạn AN, vẽ điểm M sao cho Oy là trung trực của đoạn AM.
a) Chứng minh: OM = ON
b) Tính số đo
Bài 4: Cho 2 điểm A và B nằm trên cùng một mặt phảng có bờ là đường thẳng d. Vẽ điểm C sao cho d là trung trực của đường thẳng BC, AC cắt d tai E. Trên d lấy điểm M bất kỳ.
a) So sánh MA + MB và AC
b) Tìm vị trí của M trên d để MA + MB ngắn nhất
Bài 5: Cho tam giác ABC có góc A tù. Các đường trung trực của AB và AC cắt nhau tại O và cắt BC theo thứ tự ở D và E.
a) Các tam giác ABD, ACE là tam giác gì.
b) Đường tròn tâm O bán kinh OA đi qua những điểm nào trên hình vẽ?
Bài 6: Cho tam giác ABC vuông tại A ,đương cao AH. Vẽ đường trung trục của cạnh AC cát BC tai I và cát AC tai E.
a) Chứng minh IA = IB = IC.
b) Gọi M là trung điểm của đoạn AI, chứng minh MH = ME
c) BE cắt AI tại N, tính tỉ số của đoạn MN và AI
Bài 7: Cho 4 điểm A, B, C, D phân biệt. Với điều kiện nào sau đây thì đường thẳng AC là đường trung trực của đoạn thẳng BD ?
Bài 8: Gọi M là điểm nằm trên đường trung trực của đoạn thẳng AB . Cho MA =5cm. Hỏi độ dài MB bằng ?
Bài 9: Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh ∆AMN = ∆BMN
Bài 10: Cho ba tam giác ABC, DBC, EBC có chung đáy BC . Chứng minh 3 điểm A, D, E thẳng hàng
Bài 11. Cho ΔABC cân tại A. Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của ∠ACB. Tính các góc của ΔABC
Bài 12. Cho ΔABC cân tại A , có ∠A = 40°, đường trung trực của AB cắt BC tại D . Tính ∠CAD
Bài 13. Cho ΔABC cân tại A. Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của ∠ACB. Tính các góc của ΔABC
