1. Hình thang là gì?
Hình thang trong hình học Euclide là một tứ giác có hai cạnh đối song song. Hai cạnh song song này được gọi là các cạnh đáy của hình thang, hai cạnh còn lại gọi là cạnh bên. Đường trung bình của hình thang là đoạn thẳng được nối giữa trung điểm hai cạnh bên của hình thang.
Hai góc kề một cạnh bên của hình thang luôn có tổng bằng 180°.
2. Hình thang cân là gì?
Hình thang cân là một trường hợp đặc biệt của hình thang. Theo đó, hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
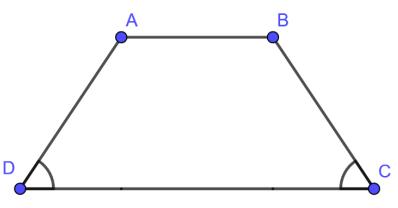
Ví dụ: ABCD là hình thang cân (đáy AB, CD) <=> AB // CD và góc C = góc D.
2. Tính chất của hình thang cân:
Tính chất 1: Trong một hình thang cân, hai cạnh bên bằng nhau:
Ví dụ: ABCD là hình thang cân (đáy AB,CD) ⇒ AD = BC.
Tính chất 2: Trong một hình thang cân, hai đường chéo bằng nhau:
Ví dụ: ABCD là hình thang cân (đáy AB,CD) ⇒ AC = BD.
Tính chất 3: Trong hình thang cân, hai góc kề 1 đáy bằng nhau:
Ví dụ: Hình thang ABCD (đáy AB,CD) ⇒ góc C= góc D và góc A = góc B.
Tính chất 4: Hình thang cân luôn nội tiếp được trong một đường tròn.
Ví dụ: ABCD là hình thang cân (AB // CD).
=> Luôn có một đường tròn tâm O nội tiếp hình thang này.
3. Dấu hiệu nhận biết hình thang cân:
Hình thang có hai góc kề một cạnh đáy bằng nhau là hình thang cân. Hình thang có hai đường chéo bằng nhau là hình thang cân.
Hình thang có hai trục đối xứng của hai đáy trùng nhau là hình thang cân
Hình thang có hai cạnh bên bằng nhau (nếu hai cạnh bên ấy không song song) là hình thang cân.
Hình thang nội tiếp đường tròn là hình thang cân.
Chú ý:
Hình thang cân thì có 2 cạnh bên bằng nhau nhưng hình thang có 2 cạnh bên bằng nhau chưa chắc đã là hình thang cân.
Trục đối xứng của hình thang cân là đường thẳng đi qua trung điểm 2 cạnh đáy của hình thang cân đó.
4. Diện tích hình thang cân:
Để tính diện tích hình thang cân ta áp dụng công thức tính diện tích hình thang như thông thường.
Diện tích hình thang bằng chiều cao nhân với trung bình cộng của hai đáy.
S = (h .(a+b))/2
Trong đó:
S là diện tích hình thang
h là chiều cao
a, b là độ dài 2 đáy
“Muốn tính diện tích hình thang
Đáy lớn, đáy bé ta đem cộng vào
Cộng vào nhân với chiều cao
Chia đôi kết quả thế nào cũng ra”
5. Chu vi hình thang cân:
Giả sử hình thang ABCD (AB//CD) cân có độ dài hai cạnh đáy là a, b và độ dài cạnh bên là c.
Khi đó, chu vi hình thang ABCD là:
P = a + b + 2c
6. Phương pháp chứng minh hình thang cân:
Để chứng minh được hình đó là hình thang cân chúng ta gồm có 3 phương pháp. Và dưới đây là chi tiết nội dung về 3 phương pháp chứng minh hình thang cân.
Phương pháp 1:
Để chứng minh tứ giác đó là hình thang cân ta phải chứng minh tứ giác đó có 2 cạnh song song với nhau dựa vào các cách chứng minh song song như sau:
– Hai góc đồng vị bằng nhau.
– Hai góc so le trong bằng nhau.
– Hai góc trong cùng phía bù nhau hoặc định lý từ góc vuông đến góc song song.
Phương pháp 2:
Chứng minh hình thang đó có hai góc kề một cạnh đáy bằng nhau thì hình thang đó là hình thang cân.
Phương pháp 3:
Chứng minh hình thang đó có hai đường chéo bằng nhau thì hình thang đó là hình thang cân.
Đây là 3 phương pháp rất hay được sử dụng để các em có thể sử đụng để làm bài tập về chứng minh hình thang cân.
7. Ứng dụng của hình thang cân trong đời sống:
Hình thang cân là 1 hình dạng phổ biến đối với mỗi con người. Và nó được dùng làm đồ chơi cho trẻ em có dạng hình thang cân. Hay hình thang cân còn được tạo ra thành những mô hình làm bằng nhựa để cho các em học sinh có thể học tập và nhận biết….. Trong thực tế, ta có thể nhìn thấy hình ảnh hình thang cân ở các vật dụng như thùng đựng rác, cái túi xách, chiếc thang,…
8. Một số bài tập về hình thang cân:
Bài tập 1: Chứng minh hình thang cân:
Ví dụ 1: Hình thang ABCD (AB // CD) có góc ACD = góc BDC. Chứng minh rằng ABCD là hình thang cân.
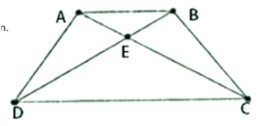
Gọi E là giao điểm của AC và BD.
Do góc ACD = góc BCD nên tam giác ECD có góc C1 = góc D1, nên là tam giác cân. Từ đó suy ra EC = ED. (1)
Tương tự do góc ACD = góc BCD và AB // CD nên tam giác EAB cân tại E, suy ra EA = EB. (2)
Từ (1) và (2) suy ra: EA + EC = EB + ED => AC = BD
Hình thang ABCD có hai đường chéo bằng nhau nên hình thang ABCD là hình thang cân (điều phải chứng minh).
Ví dụ 2: Cho hình thang cân ABCD (AB // CD), E là giao điểm của hai đường chéo. CHứng mình EA = EB, EC = ED.
Lời giải:
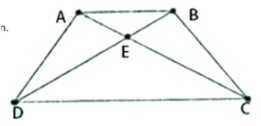
Do ABCD là hình thang cân (giả thiết) nên AD = BC, AC = BD (tính chất hình thang cân)
Xét tam giác ADC và tam giác BCD có:
AD = BC (chứng minh trên)
AC = BD (chứng mình trên)
DC chung
=> Tam giác ADC = tam giác BCD (cạnh – cạnh – cạnh)
Suy ra góc ACD = góc BDC (2 góc tương ứng)
Do đó tam giác EDC cân tại E (dấu hiệu nhận biết tam giác cân) => EC = ED (tính chất tam giac cân)
Lại có: AC = BD (chứng minh trên), EC = ED (chứng minh trên)
=> AC – CE = BD – ED => EA = EB
Vậy EA = EB và EC = ED (điều phải chứng minh).
Ví dụ 3: Cho tam giác cân ABC cân tại A, các đường phân giác BD, CE (D thuộc AC, E thuộc AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
Lời giải:
Tam giác ABC cân tại A (giả thiết) nên AB = AC và góc ABC = góc ACB (tính chất tam giác cân)
Vì BD, CE lần lượt là phân giác của góc ABC và góc ACB (giả thiết) nên theo tính chất tia phân giác:
Góc B1 = góc B2 = 1/2 của góc ABC
Góc C1 = góc C2 = 1/2 của góc ACB
Mà góc ABC = góc ACB (chứng minh trên) => góc B1 = góc B2 = góc C1 = góc C2
Xét tam giác ABD và tam giác ACE có: (1) AB = AC, (2) Góc A chung, (3) Góc B1 = góc C1 (chứng minh trên) => tam giác ABD = tam giác ACE (góc – cạnh – góc)
=> AD = AE (2 cạnh tương ứng)
Ta có: AD = AE (chứng minh trên) nên tam giác ADE cân tại A (dấu hiêu nhận biết tam giác cân) => góc AED = góc ADE (tính chất tam giác cân)
Xét tam giác ADE có: góc AED + góc ADE + góc A = 180 độ (định lý tổng ba góc trong một tam giác) => AED = (180 độ – góc A) / 2 (1)
Xét tam giác ABC có: góc A + góc ABC + góc ACB = 180 độ (định lý tổng ba góc trong một tam giác) => ABC = (180 độ – góc A) / 2 (2)
Từ (1) và (2) => góc AED = góc ABC, mà hai góc này là hai góc đồng vị nên suy ra DE // BC.
Do đó BEDC là hình thang.
Lại có góc ABC = góc ACB (chứng minh trên)
=> BEDC là hình thang cân.
Ta có: DE // BC => góc D1 = góc B2 (hai góc so le trong)
Lại có góc B2 = góc B2 (chứng minh trên) nên góc B1 = góc D1
=> Tam giác EBD cân tại E
=> EB = ED
Vậy BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
Bài tập 2: Tính diện tích hình thang cân:
Muốn tính diện tích hình thang cân, ta áp dụng công thức tính diện tích hình thang như thông thường:
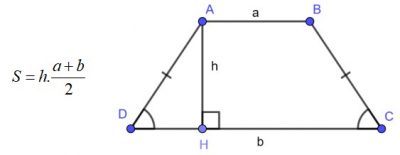
Ví dụ: Cho hình thang cân ABCD có đáy nhỏ AB = 5 cm, đáy lớn DC dài gấp đôi đáy nhỏ. Chiều cao của hình thang AH = 6 cm. Tính diện tích hình thang cân ABCD.
Lời giải:
Theo đề bài ta có: AB = 5 cm.
DC dài gấp đôi AB, suy ra DC = 10 cm.
AH = 6 cm.
Áp dụng ngay công thức tính diện tích hình thang ta được phép tính:
S = 1⁄2 h (a + b) = 1⁄2 x 6 x (5 + 10) = 40 cm2.
Vậy diện tích hình thang cân ABCD là 40 cm2.
Bài tập 3: Tính chu vi hình thang cân:
Công thức tính chu vi hình thang cân ABCD (AB, DC là cạnh đáy) là:
P = AB + DC + 2. AD
Ví dụ: Tính chu vi của hình thang cân ABCD, biết rằng AB = 4 cm; DC = 12 cm; AD = 5 cm.
Lời giải:
Áp dụng công thức tính chu vi hình thang, ta có:
Chu vi hình thang cân ABCD là : P (ABCD) = 4 + 12 + 2.5 = 26 cm.
Vậy chu vi hình thang cân ABCD là 26 cm.
Bài tập 4: Chứng minh hình thang cân nội tiếp đường tròn:
Tính chất 4 ở phần tính chất hình thang cân đã nói rằng ” Hình thang cân luôn nội tiếp được trong một đường tròn”. Và chiều ngược lại cũng đúng, tức: Một hình thang nội tiếp đường tròn là hình thang cân.
Lời giải:
Cách 1:

Ta có ABCD là hình thang, suy ra góc A1 = góc C1 (AD//BC). nên sđCD = sđAB, suy ra sđ BAD = sđADC, do đó góc ABC = góc DCB. Tức là ABCD là hình thang cân.
Cách 2:
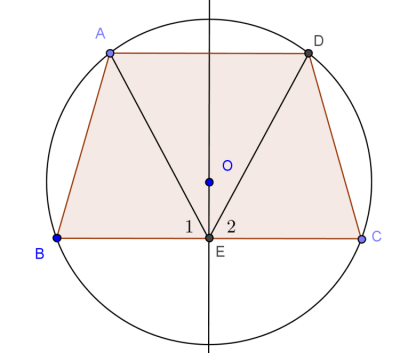
Gọi E là trung điểm BC, dễ chỉ ra được OE là trung trực của BC và AD (Do OA=OB=OC=OD). Từ đó chứng minh được góc E1 = góc E2, nên tam giác ABE = tam giác DCE (c.g.c) . Do đó góc ABC = góc DCB, suy ra ABCD là hình thang cân (điều phải chứng minh).
