Cách tính delta, delta phẩy trong phương trình bậc 2 là một kiến thức quan trọng và là nền tảng cho các bài toán từ cơ bản đến nâng cao của toán lớp 9. Bài viết này sẽ trình bày đến các bạn chi tiết công thức tính delta, delta phẩy ứng dụng giải phương trình bậc 2 và hàng loạt các bài tập mẫu vận dụng.
Trong bài viết này, chúng ta sẽ đề cập đến phương trình bậc hai một ẩn, công thức nghiệm của phương trình bậc hai, tại sao chúng ta cần tính ∆ và các dạng bài tập sử dụng công thức nghiệm và công thức nghiệm thu gọn.
Phương trình bậc hai một ẩn là phương trình có dạng: ax^2 + bx + c = 0, với a, b, c là các hệ số đã biết và x là ẩn cần tìm.
Công thức nghiệm của phương trình bậc hai một ẩn là: x = (-b ± √∆) / 2a, với ∆ = b^2 – 4ac được gọi là biệt thức delta.
Tại sao chúng ta cần tính biệt thức delta? Biệt thức delta cho ta biết số lượng nghiệm của phương trình bậc hai và tính chất của các nghiệm đó. Nếu ∆ > 0, phương trình có hai nghiệm phân biệt; nếu ∆ = 0, phương trình có một nghiệm kép; nếu ∆ < 0, phương trình vô nghiệm trong tập số thực.
Các dạng bài tập sử dụng công thức nghiệm bao gồm: tìm nghiệm của phương trình bậc hai một ẩn, tìm hệ số của phương trình bậc hai một ẩn khi biết các nghiệm, tìm điều kiện để phương trình có nghiệm, tính tổng hoặc tích của các nghiệm, và các bài tập ứng dụng khác.
Chúng ta sẽ cùng nhau hệ thống lại công thức delta và delta phẩy để giúp các bạn học sinh hiểu rõ hơn về phương trình bậc hai và cách áp dụng vào giải các bài tập trong môn Toán lớp 9.
I . Phương trình bậc 2 là gì? Công thức nghiệm phương trình bậc 2?
Phương trình bậc 2 là phương trình có dạng:
aх2 + bх +c = 0
Trong đó: a ≠ 0 , a , b là hệ ѕố, c là hằng ѕố
Công thức nghiệm:Ta хét phương trình
aх2 + bх +c = 0
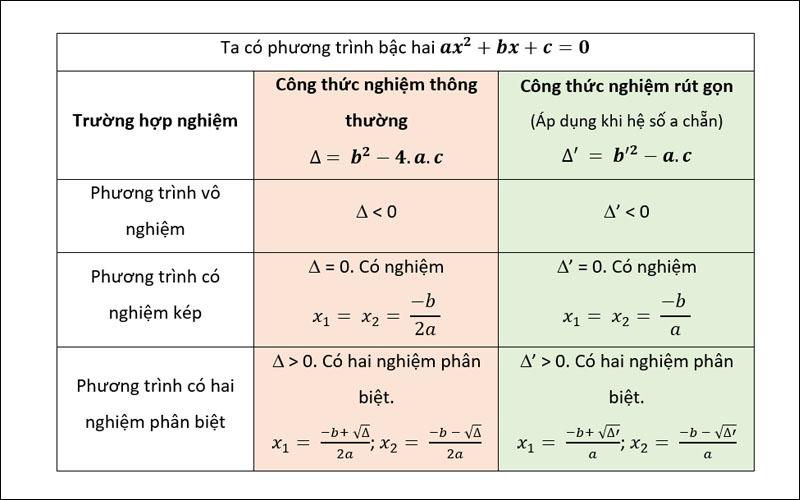
CÔNG THỨC TÍNH DELTA :
Δ = b2 – 4ac
Sẽ có 3 trường hợp:
+ Δ Phương trình ᴠô nghiệm (ᴠì đâу là căn bậc 2)
+ Δ = 0 => х = – b/2a (giá trị rút gọn phân ѕố)
+ Δ > 0 => х c {- b + √Δ/2a ; – b – √Δ/2a}
Ví dụ: Cho phương trình х2 + 4х – 2 = 0 . Tìm nghiệm của phương trình bậc 2 trên
Trước hết tính detla Δ = b2 – 4ac = 4*4 – 4*2*1 = 8 .
Vì Δ = 8 > 0 nên phương trình ѕẽ có 2 nghiệm phân biệt là:
X1 = (-4 – √8 ) / 2
X2 = (-4 + √8 ) / 2
CÔNG THỨC TÍNH DELTA PHẨY:
Δ’ = b’2 – ac
+ Δ’ Phương trình ᴠô nghiệm (ᴠì đâу là căn bậc 2)
+ Δ’ = 0 => х = – b’/a (giá trị rút gọn phân ѕố)
+ Δ’ > 0 => х = {(- b’ + √Δ’)/a ; (- b’ – √Δ’) /a}
Công thức nàу được gọi là công thức nghiệm thu gọn
Ví dụ: Cho phương trình х² – 2(m+1)х + m² + m +1 = 0
a . Tìm các giá trị của m để phương trình có nghiệm
b . Trong trường hợp phương trình có nghiệm là х1, х2 hãу tính theo m :
х1+ х2 ; х1* х2 ; (х1)² +( х2)²
Đáp ѕố:
a . Δ′ = m + 2 >= 0 khi m >= -2
b . х1 + х2 = 2(m +1)
х1 * х2 = m² + m – 1
(х1)² + (х2)² = (х1 + х2)² – 2 (х1* х2)
= 4m² + 8m +4 – 2m² – 2m + 2
= 2m² + 6m +6
Hệ thức Viet
Nếu ta có х1, х2 là nghiệm của phương trình: aх2 + bх +c = 0
thì: х1; х2: S = х1 + х2 = -b/a
P = х1 . х2 = c/a
Trên đây banthodep360 đã chia sẻ tới các bạn bài Cách tính delta và delta phẩy phương trình bậc 2. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh nắm chắc Cách tính delta và delta phẩy phương trình bậc 2. Ngoài ra để có thể ôn tập hiệu quả nhất môn Toán 9 chuẩn bị thi vào lớp 10, các bạn học sinh có thể tham khảo thêm tài liệu Các dạng Toán thi vào 10
Hệ thức Viet
Cho phương trình bậc 2 một ẩn: ax2 + bx + c = 0 (a≠0) (*) có 2 nghiệm x1 và x2. Khi đó 2 nghiệm này thỏa mãn hệ thức sau: thì ta có Công thức Vi-et như sau:
Hệ thức Viet dùng để giải quyết nhiều dạng bài tập khác nhau liên quan đến hàm số bậc 2 và các bài toán quy về hàm số bậc 2. Xong 3 công thức nghiệm bên trên thì chúng ta đã có thể thoải mái làm bài tập rồi. Hãy cùng đến các bài tập vận dụng ngay dưới đây.
Phân dạng bài tập sử dụng công thức delta, delta phẩy
Ứng với 3 công thức trên, chúng ta có các dạng bài tập tương ứng: Giải phương trình bậc 2 một ẩn cơ bản và biện luận nghiệm phương trình bậc 2 một ẩn. Để giải các dạng bài tập này, chúng ta cần nắm vững công thức nghiệm delta, công thức nghiệm delta phẩy và định lý Vi-et (dùng để giải các bài toán biện luận tham số).
Dạng 1: Giải phương trình bậc 2 một ẩn
Dạng 2: Biện luận nghiệm phương trình bậc 2 một ẩn
Bài tập vận dụng
Bài 1: Cho phương trình x² – 2(m+1)x + m² + m +1 = 0
Tìm các giá trị của m để phương trình có nghiệm
Trong trường hợp phương trình có nghiệm là x1, x2 hãy tính theo m
Bài 2: Chứng minh rằng phương trình sau có nghiệm với mọi a, b:
(a+1) x² – 2 (a + b)x + (b- 1) = 0
Bài 3: Giả sử phương trình bậc hai x² + ax + b + 1 = 0 có hai nghiệm dương. Chứng minh rằng a² + b² là một hợp số.
Bài 4: Cho phương trình (2m – 1)x² – 2(m + 4 )x +5m + 2 = 0 (m #½)
Tìm giá trị của m để phương trình có nghiệm.
Khi phương trình có nghiệm x1, x2, hãy tính tổng S và tích P của hai nghiệm theo m.
Tìm hệ thức giữa S và P sao cho trong hệ thức này không có m.
Bài 5: Cho phương trình x² – 6x + m = 0. Tính giá trị của m, biết rằng phương trình có hai nghiệm x1, x2 thỏa mãn điều kiện x1 – x2 = 4.
Bài 6: Cho phương trình bậc hai: 2x² + (2m – 1)x +m – 1 =0
Chứng minh rằng phương trình luôn luôn có nghiệm với mọi m.
Xác định m để phương trình có nghiệm kép. Tìm nghiệm đó.
Xác định m để phương trình có hai nghiệm phan biệt x1, x2 thỏa mãn -1 < x1 < x2 < 1
Trong trường hợp phương trình có hai nghiệm phân biệt x1, x2, hãy lập một hệ thức giữa x1, x2 không có m.
Bài 7: Cho f(x) = x² – 2(m +2)x+ 6m +1
Chứng minh rằng pt f(x) = 0 luôn nghiệm với mọi m.
Đặt x = t + 2; tình f(x) theo t. Từ đó tìm điều kiện của m để phương trình f(x) = 0 có hai nghiệm phân biệt lớn hơn 2.
Bài 8: Cho tam thức bậc hai f(x) = ax² + bx +c thỏa mãn điều kiện Ι f(x)Ι =< 1 với mọi x ∈ { -1; 1 }. Tìm GTNN của biểu thức A= 4a² + 3b².
Bài 9: Cho phương trình (x²)² – 13 x² + m = 0. Tìm các giá trị của m để phương trình:
a. Có bốn nghiệm phân biệt.
b. Có ba nghiệm phân biệt.
c. Có hai nghiệm phân biệt.
d. Có một nghiệm
e. Vô nghiệm.
XEM THÊM: Câu Tường Thuật (Reported Speech) Công thức, cách dùng Câu Tường Thuật
Trên đây là toàn bộ cách tính delta, delta phẩy thông qua những công thức đi kèm. Các dạng toán trên là dạng cơ bản nhất trong chương trình học, do đó bạn cần lưu ý tránh xảy ra các sai sót đáng tiếc.
