Công thức tính diện tích hình tròn là một trong những công thức cơ bản chúng ta đã được học từ khi còn ngồi trên ghế nhà trường. Tuy nhiên, đây cũng là kiến thức mới đối với các em học sinh lớp 5. Hãy cùng INVERT tìm hiểu diện tích hình tròn là gì, công thức tính diện & cách vận dụng các bài tập, thông qua bài viết sau.

Hình tròn là gì? Diện tích hình tròn là gì?
Hình tròn trong hình học phẳng là một hình bị giới hạn bởi một đường tròn. Trong đó, tâm, bán kính và chu vi của hình tròn chính là tâm, bán kính của đường tròn bao quanh nó.
Diện tích hình tròn là toàn bộ phần diện tích nằm bên trong đường tròn, được nghiên cứu bởi người Hy Lạp cổ đại. Nghiên cứu chỉ ra rằng, diện tích hình tròn tỉ lệ thuận với bình phương bán kính của nó.
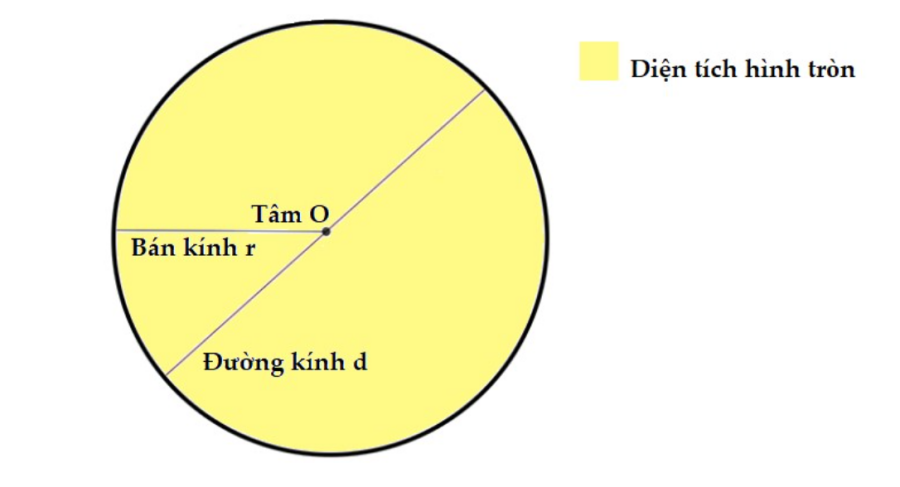
Công thức tính diện tích hình tròn lớp 5
Diện tích hình tròn được tính theo công thức như sau: Bán kính nhân bán kính) nhân với số pi (3,14) hay bình phương bán kính hình tròn nhân với PI.
Công thức: S = R x R x 3,14 Hoặc bạn có thể tính diện tích hình tròn khi biết đường kính bằng công thức:

Trong đó:
- S: là kí hiệu đại diện cho diện tích đường tròn
- π: là kí hiệu sô pi, với π = 3,14
- R: là bán kính hình tròn
- D: là đường kính hình tròn
Công thức tính diện tích hình quạt tròn:
Diện tích của hình quạt tròn S có thể được tính bằng công thức sau:
Trong đó:
- θ là góc tạo bởi hai bán kính (đo bằng radian).
- R là bán kính của hình tròn.
Để tính diện tích hình quạt tròn S chắn bởi hai bán kính tạo thành góc n° trong một hình tròn bán kính R và độ dài cung tròn l, chúng ta có thể sử dụng công thức sau:
Trong đó:
- n là góc tạo bởi hai bán kính (đơn vị đo là độ).
- R là bán kính của hình tròn.
Ví dụ: Hãy tính diện tích một hình quạt tròn có bán kính 6cm, có số đo cung là 36 độ.
Giải: Áp dụng công thức tính diện tích hình quạt tròn, ta có:

Tính chất của hình tròn lớp 5 cần nắm
Tính chất của hình tròn có thể được diễn đạt một cách ngắn gọn và súc tích hơn như sau:
- Đường kính: Đường kính là đoạn thẳng lớn nhất đi qua hình tròn và chia nó thành hai nửa bằng nhau. Độ dài đường kính bằng gấp đôi bán kính.
- Chu vi: Hai đường tròn bằng nhau sẽ có chu vi bằng nhau. Chu vi của một đường tròn tỷ lệ thuận với bán kính của nó.
- Bán kính: Khi hai đường tròn bằng nhau, bán kính của chúng cũng bằng nhau và ngược lại. Bán kính là đoạn thẳng từ tâm đến bất kỳ điểm nào trên đường tròn.
- Góc tại tâm: Góc tại tâm của đường tròn là 360 độ, tức là một vòng tròn đầy đủ.
- Tiếp tuyến: Hai tiếp tuyến được vẽ từ một điểm bên ngoài trên đường tròn sẽ có độ dài bằng nhau. Một tiếp tuyến tạo thành góc vuông với bán kính tại điểm tiếp xúc.
- Đối xứng: Đường tròn có tính đối xứng, có trục đối xứng đi qua tâm và tất cả các điểm trên đường tròn sẽ có một điểm đối xứng so với tâm.
Hướng dẫn cách tính diện tích hình tròn
1. Tính diện tích hình tròn theo bán kính
Bước 1: Đầu tiên, xác định bán kính của hình tròn
Bán kính là khoảng cách không đổi từ tâm đến cạnh của hình tròn. Hay nói cách khác bán kính chính là 1 nửa đường kính của hình tròn.
Thông thường đề bài sẽ cho sẳn bán kính. Nếu không cũng sẽ cho đường kính để bạn suy ra được bán kính. Giả sử, đề bài cho bạn bán kính là 6 cm.
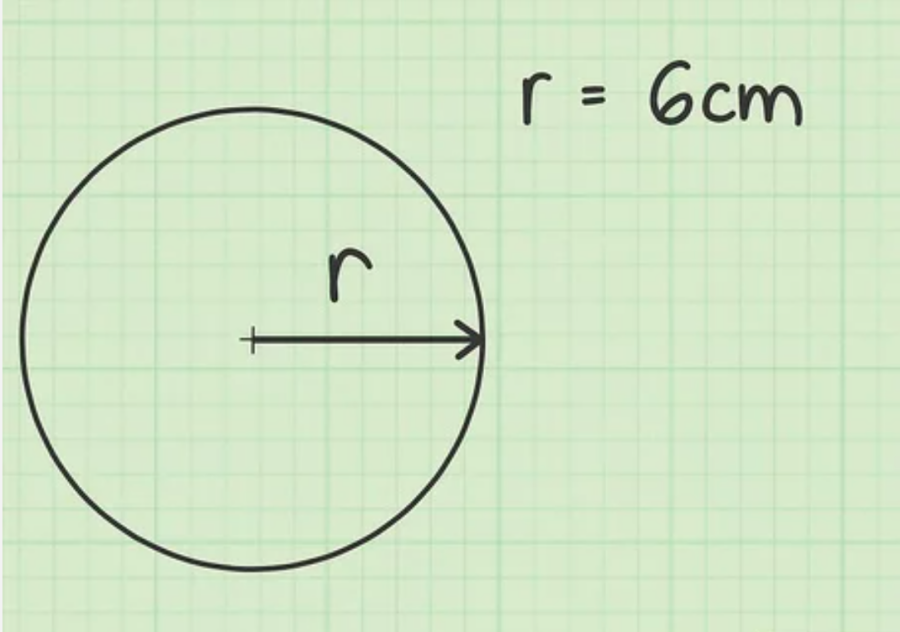
Bước 2: Tiếp theo, bạn tính bình phương bán kính
Tiếp tục, bạn thay r vào công thức tính diện tích hình tròn: A = π. r. r =
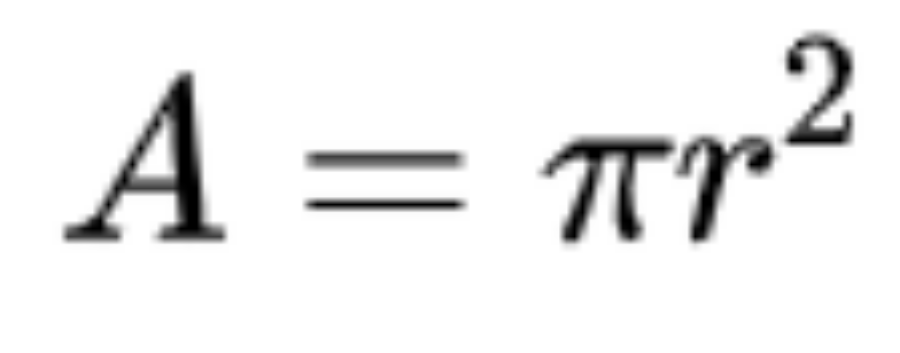
Theo như giả sử trên, hình tròn có bán kính là 6 cm (r = 6). Suy ra:
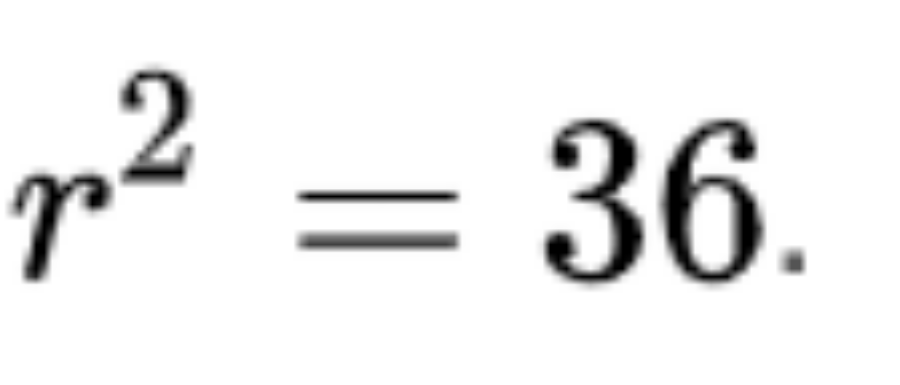
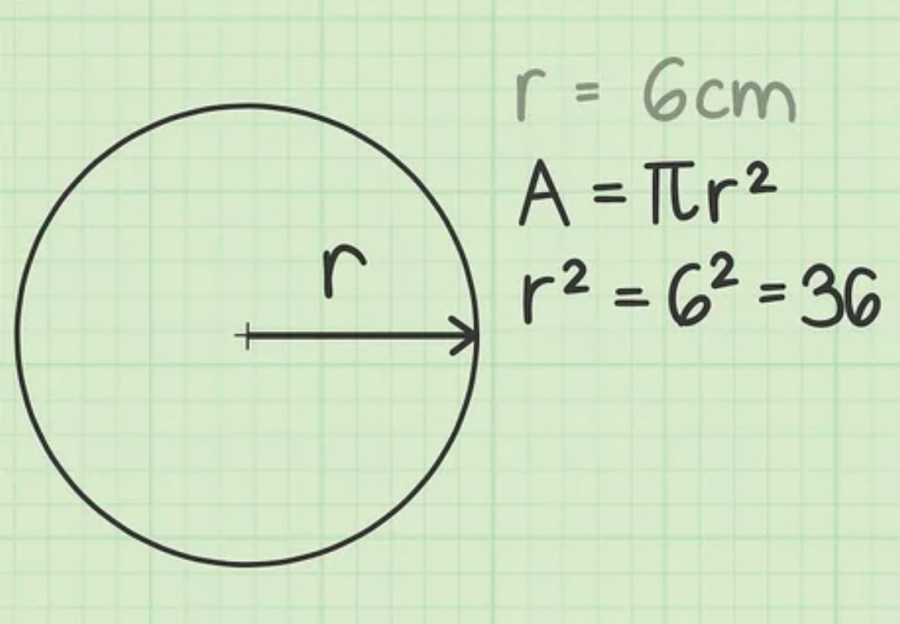
Bước 3: Sau đó, nhân với hệ số pi
Pi (π) là 1 hằng số đại diện cho tỉ lệ giữa chu vi và đường kính hình tròn. Pi được ký hiệu bằng chữ cái Hy lạp và gần bằng giá trị 3,14.
Với ví dụ trên, đường tròn có bán kính r = 6 thì diện tích hình tròn được tính như sau:
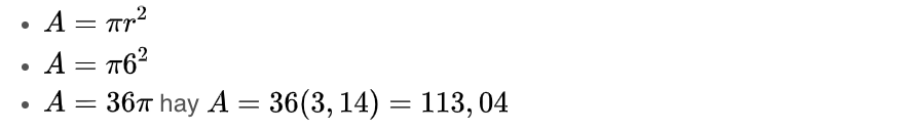
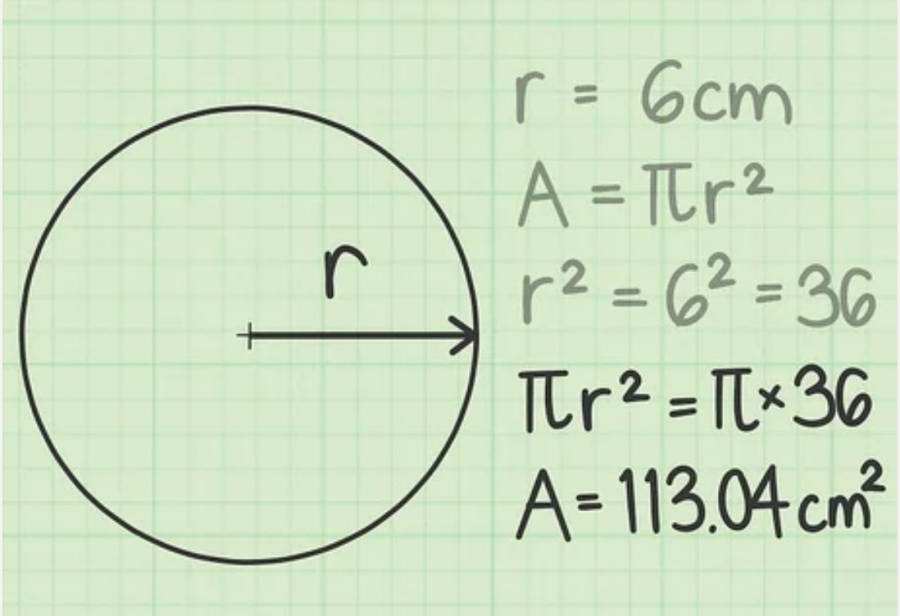
Bước 4: Cuối cùng, trình bày đáp án
Lưu ý khi đơn vị của diện tích luôn luôn kèm theo dấu bình phương hay còn được gọi là vuông. Ví dụ như bán kính được tính bằng xăng-ti-mét, diện tích sẽ là xăng-ti-mét vuông. Ngoài ra, bạn cũng có thể trình bày đáp án theo 2 cách:
Đối với hình tròn có bán kính 6 cm, diện tích sẽ là:

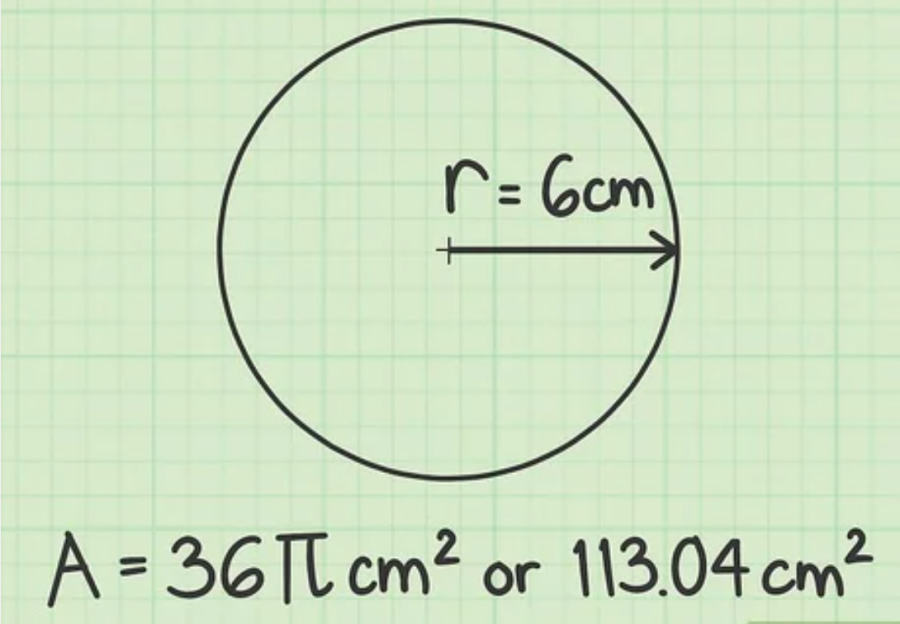
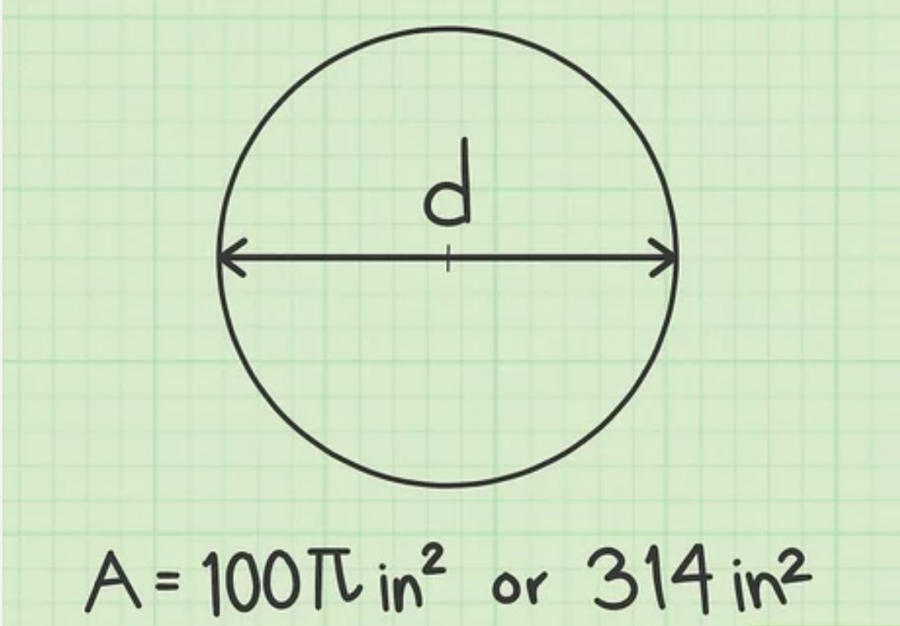
2. Tính diện tích hình tròn theo đường kính
Cách tính diện tích hình tròn khi biết đường kính lớp 5:
Bước 1: Trước tiên, đo hay viết lại đường kính
Trong 1 số bài toán, đề sẽ không cho sẳn bán kính mà cho đường kính để từ đó suy ra bán kính. Bạn có thể dùng thước đo đường kính nếu nó được vẽ trong sơ đồ bài toán.
Giả sử, bạn có đường kính của hình tròn là 20 cm.
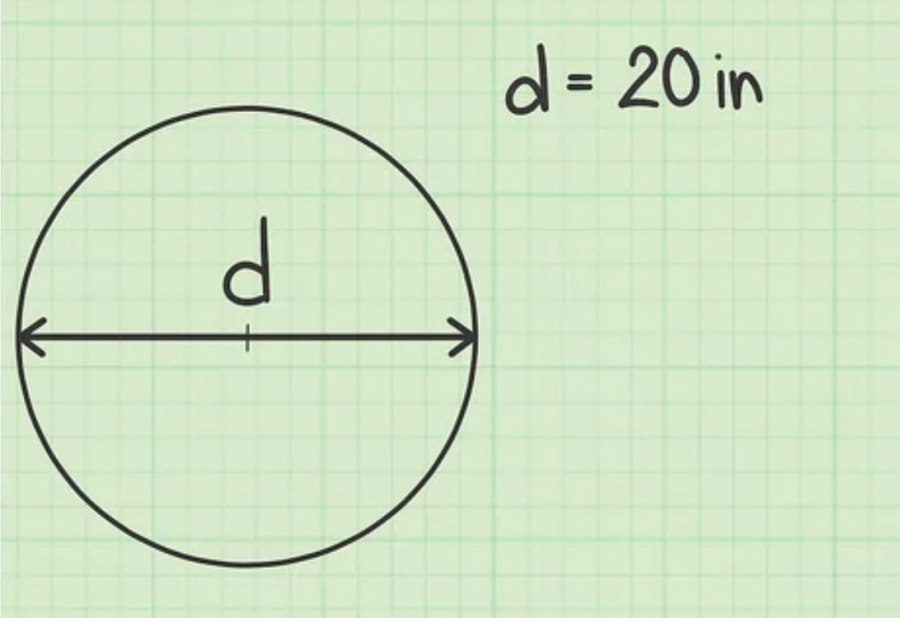
Bước 2: Tiếp theo, chia đôi đường kính
Theo định nghĩa, đường kính dài bằng 2 lần bán kính. Bạn chỉ việc lấy đường kính chia 2 là ra bán kính.
Theo ví giả sử trên, hình tròn có đường kính 20 cm sẽ cho ra bán kính là 20/2 = 10 cm.
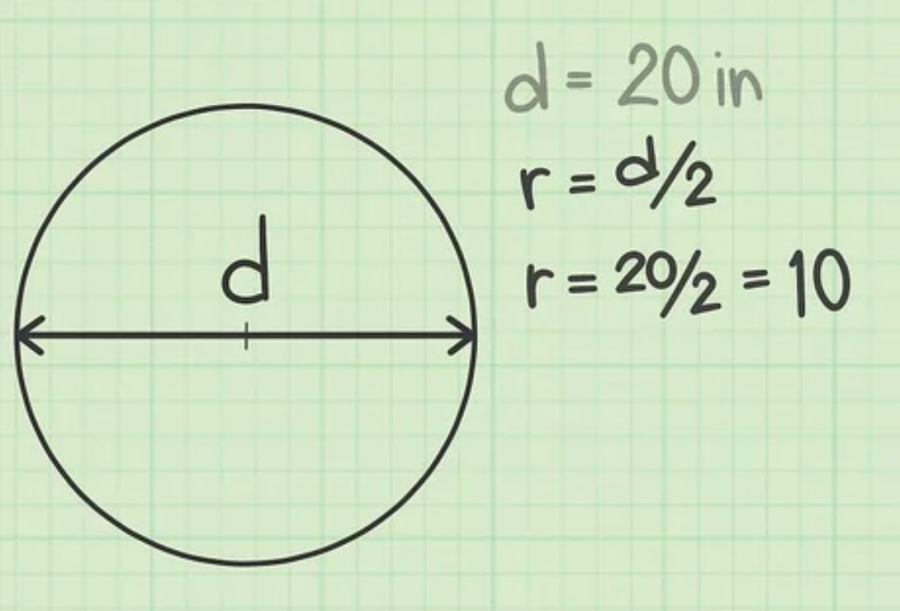
Bước 3: Sau đó, áp dụng công thức dính diện tích cơ bản
Sau khi tính được bán kính từ đường kính, bạn áp dụng vào công thức tính diện tích hình tròn. Sau đó gán các giá trị của bán kính, ta được:
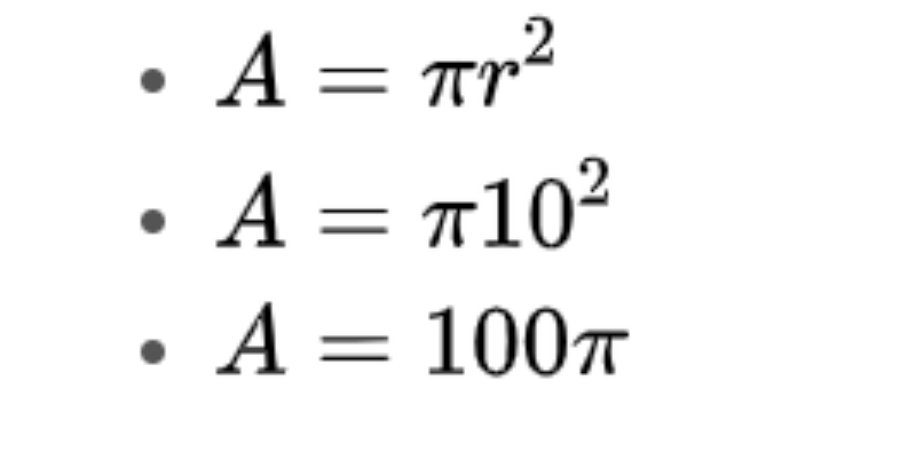
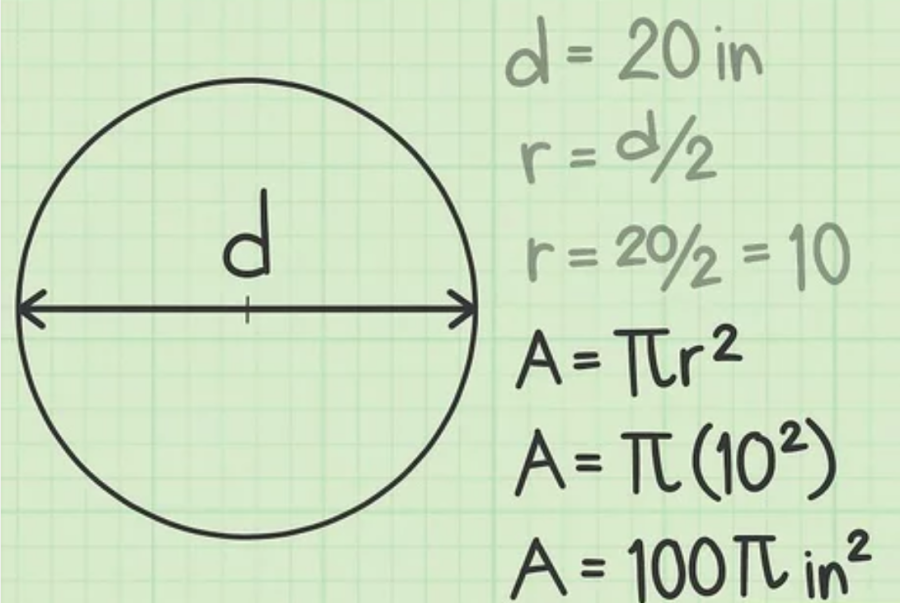
Bước 4: Cuối cùng, trình bày giá trị của diện tích
Đơn vị diện tích của hình tròn sẽ được trình bày đi cùng với dấu “bình phương”.
Trong ví dụ này, đường kính được tính bằng cm -> bán kính cũng được tính bằng cm. Vậy nên, diện tích hình tròn sẽ được tính theo cm vuông, tức là:
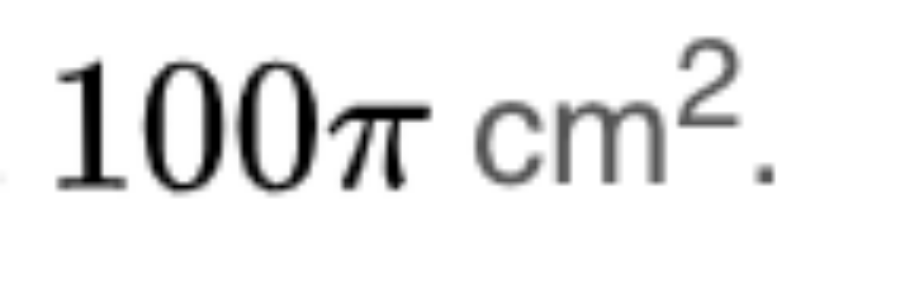
Hay bạn cũng có thể thay số pi để tính ra kết quả:
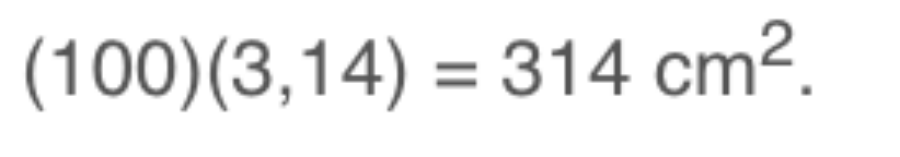
3. Tính diện tích hình tròn theo chu vi
Bước 1: Trước tiên, tìm hiểu về công thức biến đổi
Bạn có thể dùng công thức biến đổi để tìm diện tích hình tròn nếu đã biết chu vi của nó. Đối với công thức biến đổi này bạn không cần phải tìm bán kính mà nó sẽ gán thẳng giá trị chu vi để tính diện tích.
Công thức tính diện tích hình tròn theo chu vi:
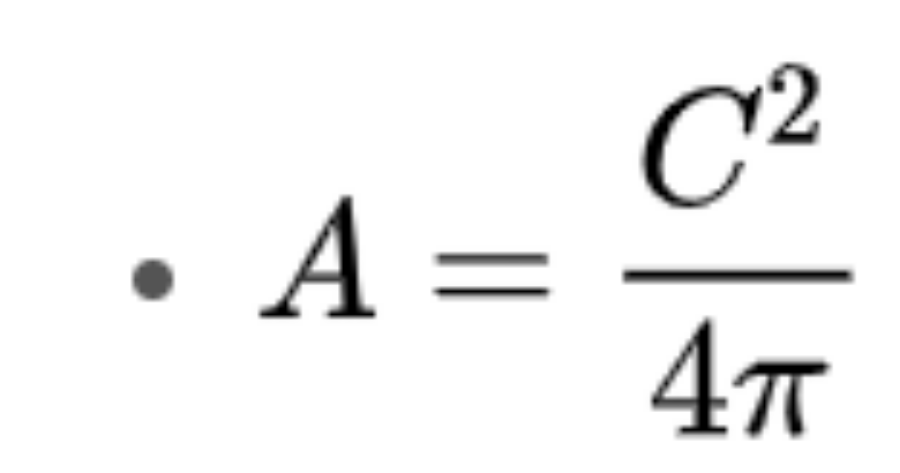
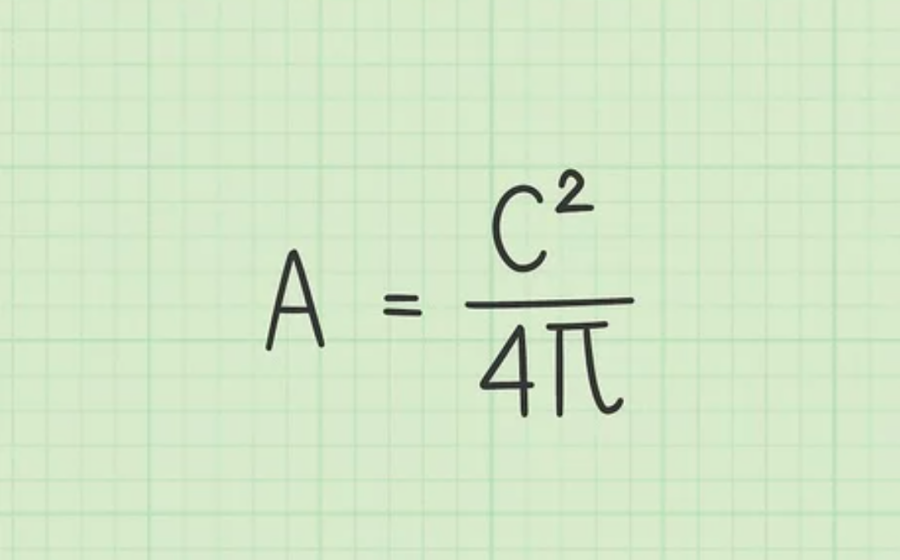
Bước 2: Sau đó, đo hoặc viết ra chu vi
Trong một số trường hợp bạn sẽ không thể nào đo chính xác đường kính hay bán kính được. Ví dụ đối với một số vật thể có hình tròn như 1 chiếc chảo nướng pizza hay chảo rán bạn có thể dùng thước dây để đo chu vi vì nó chính xác hơn nhiều việc bạn đo đường kính.
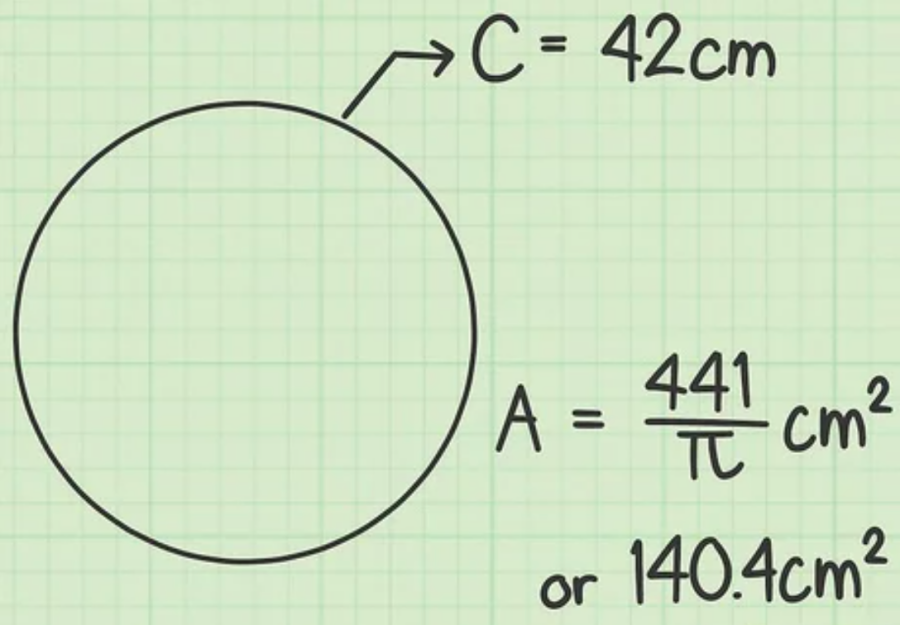
Giả sử bạn có hình tròn (hay một vật hình tròn) với chu vi là 42 cm.
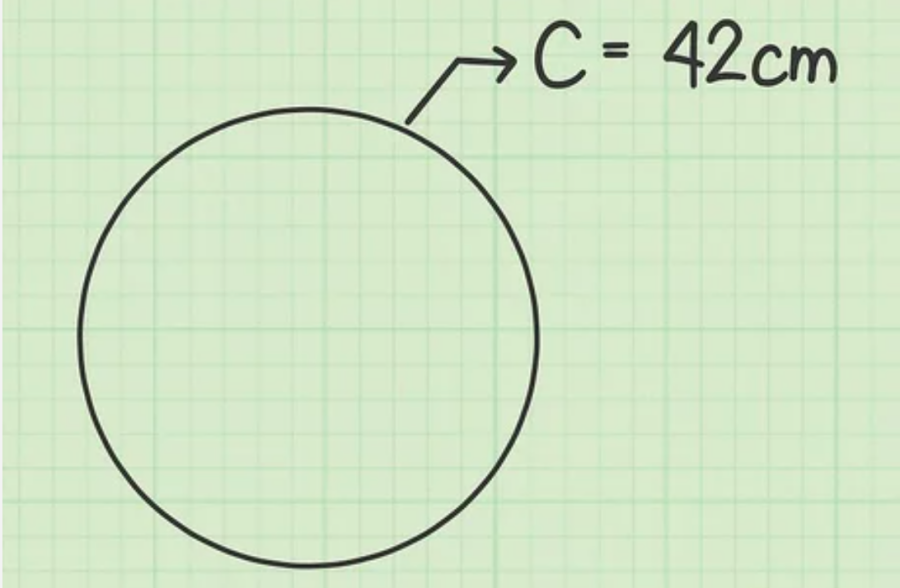
Bước 3: Tiếp theo, sử dụng mối quan hệ giữa chu vi và bán kính để biến đổi công thức
Chu vi của một đường tròn bằng pi nhân với đường kính (C = π.d) và d = 2r. Từ đó suy ra: C = π.2.r, ta có:


Bước 4: Tiếp đến, thay vào công thức tính diện tích hình tròn
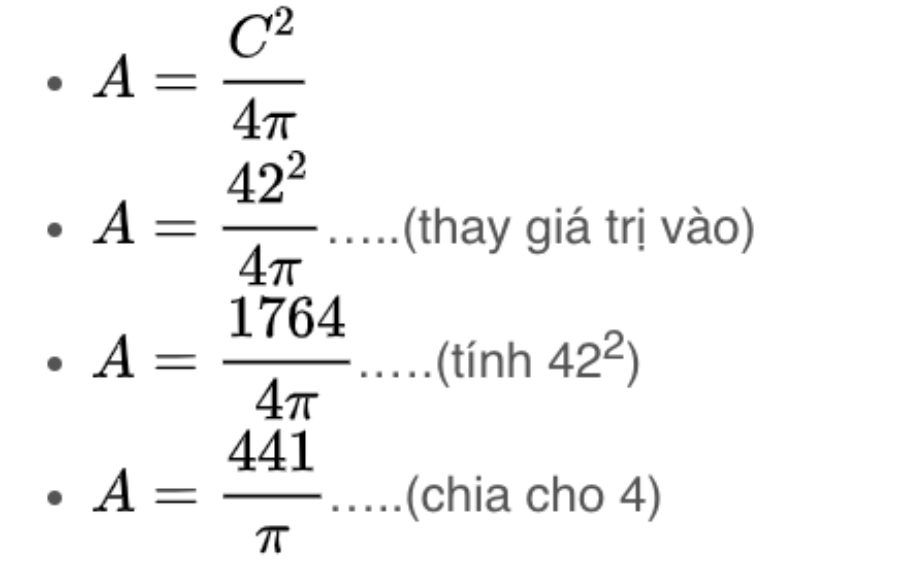
Nhằm tận dụng mối quan hệ giữa chu vi và bán kính, bạn thay vào công thức biến đổi để ra được kết quả như sau:


Bước 5: Kế tiếp, áp dụng công thức biến đổi để tính diện tích
Bạn tiến hành gán chu vi vào công thức biến đổi thay vì dùng công thức có chứa bán kính. Trong ví dụ này, bạn gắn chu vi là 20 cm vào để ra được kết quả như dưới đây:
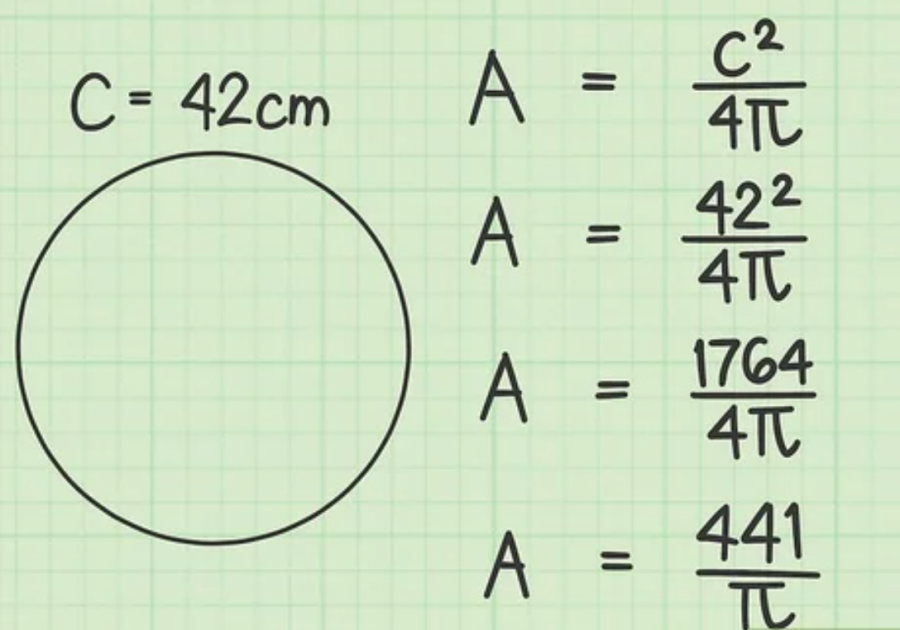
Bước 6: Đưa ra đáp án cuối cùng
Bạn có thể trình bày đáp số theo 2 cách. Hai cách này đều đúng nhưng tuỳ theo yêu cầu của đề bài mà bạn nên trình bày cho phù hợp.

4. Tính diện tích hình tròn bằng hình quạt
Bước 1: Trước tiên, xác định thông tin đã biết
Một số bài toán sẽ cho bạn số liệu về hình quạt của hình tròn, sau đó đề bài sẽ yêu cầu bạn tính diện tích toàn phần của hình tròn đó. Một số đề khác lại cho các thông tin tương tự như: Một hình quạt của hình tròn O có diện tích là 15 π (cm2). Hãy tính diên tích của hình tròn tâm O.
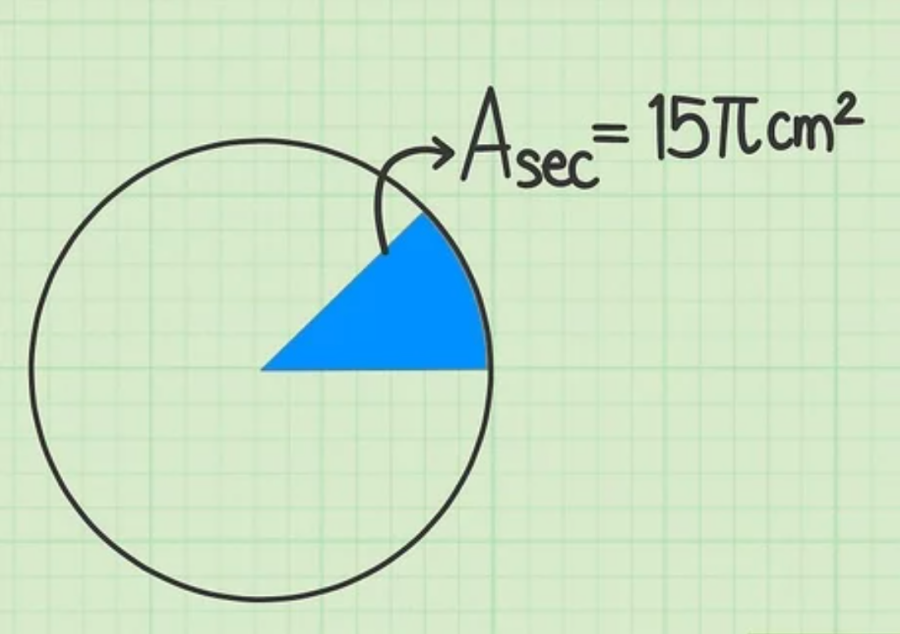
Bước 2: Sau đó, xác định hình quạt đã cho
Hình quạt là 1 phần chia của hình tròn và được xác định bằng cách vẽ 2 đường bán kính từ tâm đến cạnh của đường tròn. Khi đó khoảng trống giữa hai bán kính đó chính là hình quạt.
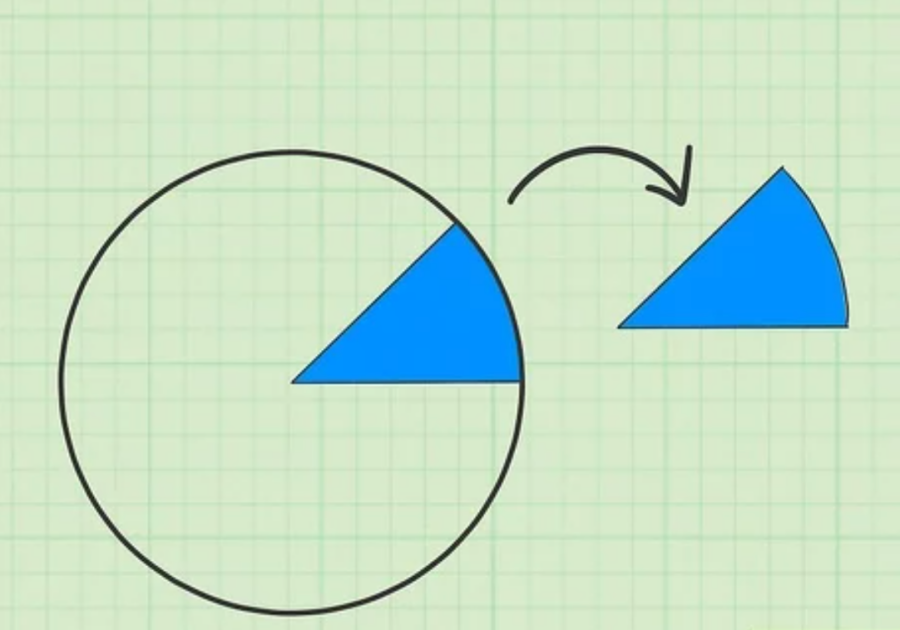
Bước 3: Tiếp theo, tính góc ở tâm của hình quạt
Tới đây, bạn dùng thước đo góc để đo góc giữa tạo ra bởi 2 bán kính. Cách đo như sau: Bạn đặt cạnh đáy của thước đo góc dọc theo 1 đường bán kính, trung tâm của thước trùng với tâm hình tròn khi đó số đo góc là vị trí của bán kính thứ 2 tạo thành hình quạt.
- Lưu ý, bạn hãy đo đúng góc nhỏ giữa 2 bán kính chứ không phải đo góc lớn hơn nằm phía ngoài. Thường thì tổng của góc nhỏ và góc lớn sẽ là 360 độ.
- Trong một số bài toán, đề bài sẽ cho sẳn số đo góc. Ví dụ: “Góc ở tâm của hình quạt là 45 độ”, nếu như không có số liệu, bạn phải tiến hành đo.
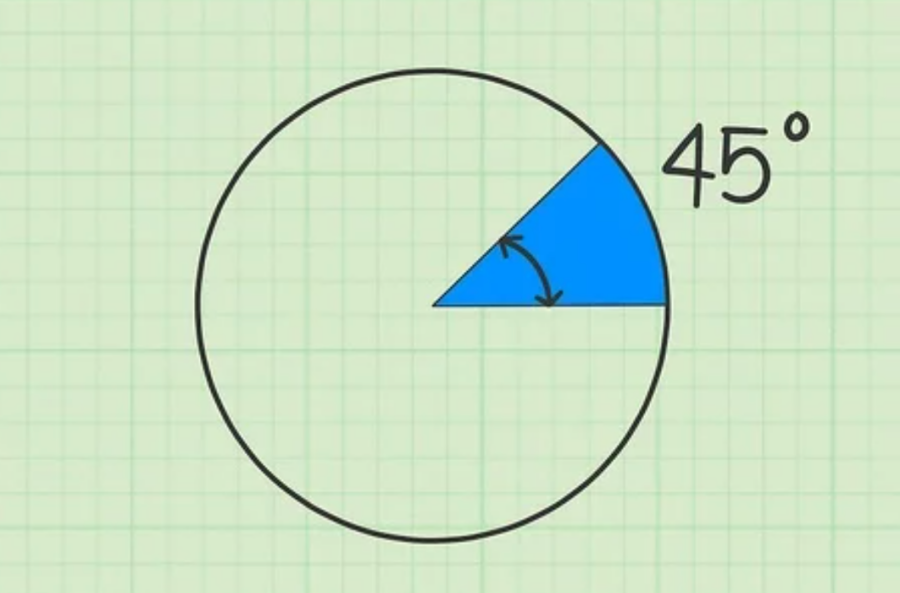
Bước 4: Tiếp đến, áp dụng công thức biến đổi để tính diện tích
Khi đã biết diện tích của hình quạt và số đo góc ở tâm, bạn có thể áp dụng công thức biến đổi để tìm diện tích của hình tròn như sau:

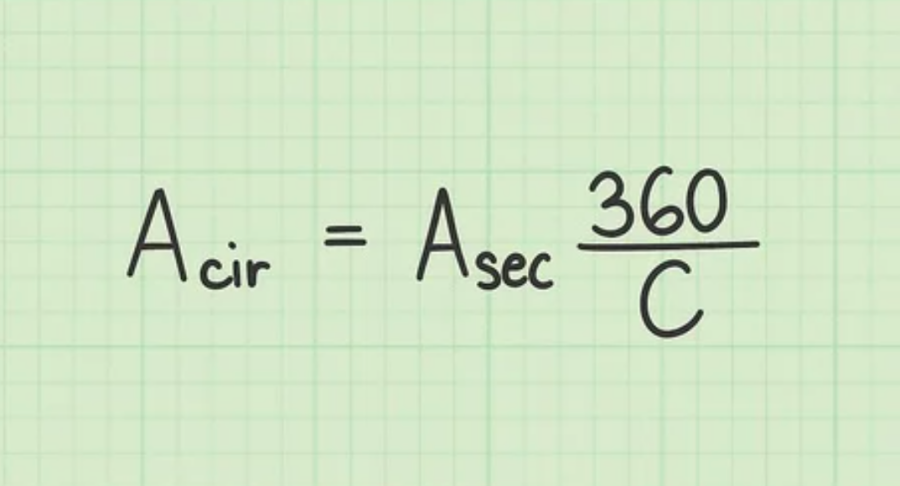
Bước 5: Kế tiếp, nhập các giá trị mà bạn biết và tính diện tích
Giả sử, bạn có góc ở tâm là 45 độ, diện tích hình quạt là 15 π. Sau đó, bạn thay vào công thức để ra kết quả như sau:
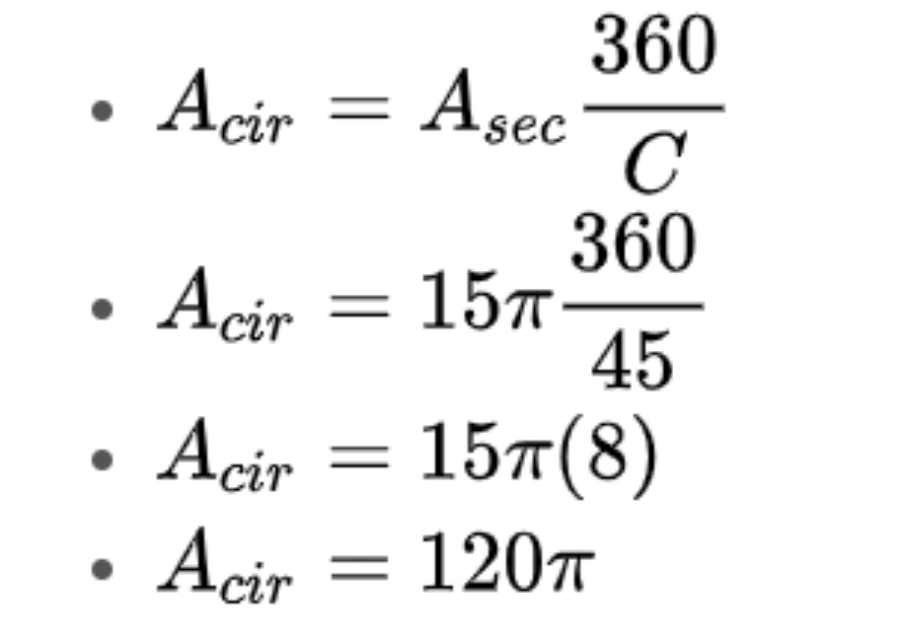

Bước 6: Đưa ra đáp án là xong
Trong ví dụ đã cho, hình quạt bằng 1/8 diện tích toàn phần của hình tròn. Từ đó suy ra diện tích toàn phần của hình tròn là 120π (cm2) hay 120 x 3.14 = 376,8 (cm2)
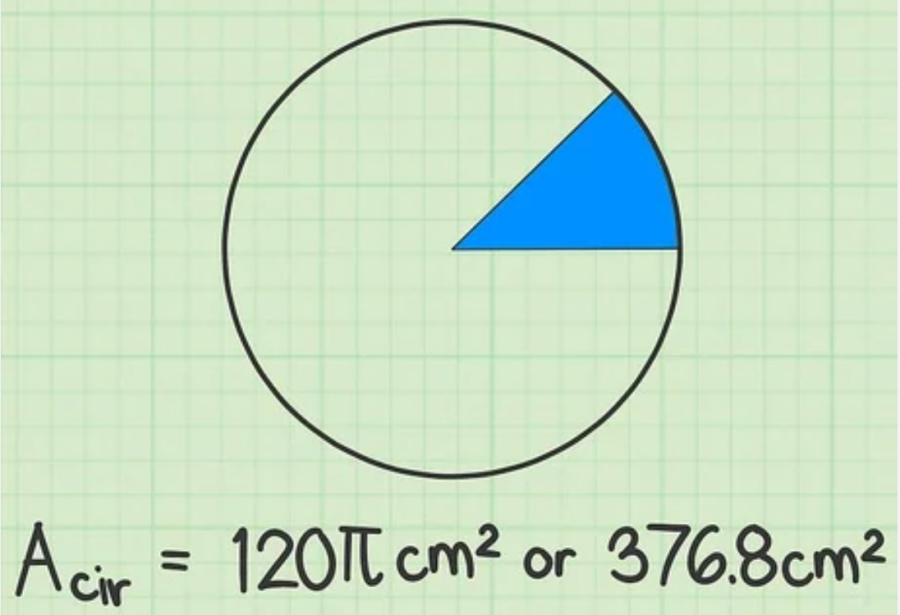
Một số bài tập tính diện tích hình tròn lớp 5
1. Bài tập tính diện tích hình tròn có lời giải
Câu 1: Tính diện tích hình tròn có bán kính bằng 5cm.
Giải: Diện tích hình tròn là: 5 x 5 x 3,14 = 78,5 (cm2)
Câu 2: Tính diện tích hình tròn có đường kính d=12cm
Giải: Bán kính hình tròn là: 12 : 2 = 6 (cm) -> Diện tích hình tròn là: 6 x 6 x 3,14 = 113,04 (cm2)
Câu 3: Tính diện tích hình tròn có chu vi bằng 31,4cm.
Giải: Bán kính hình tròn là: 31,4 : 3,14 : 2 = 5 (cm) -> Diện tích hình tròn là: 5 x 5 x 3,14 = 78,5 (cm2)
Câu 4: Cho hình tròn C có đường kính d = 16 cm. Hãy tính S(diện tích) hình tròn C?
Giải: Ta có, bán kính bằng một nữa đường kính theo công thức: R = d/2
<=> R = 16/2 = 8 cm
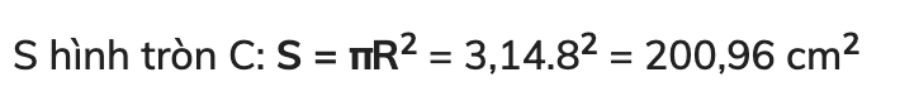
Câu 5: Tính diện tích toàn bộ hình vẽ bên dưới?
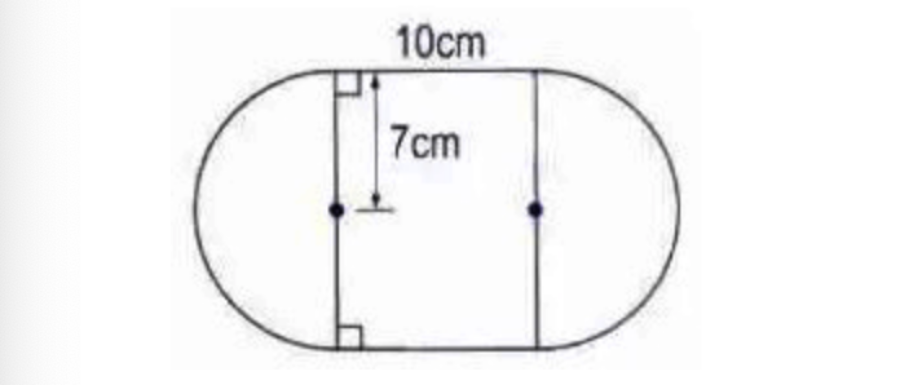
Giải: Ta thấy, diện tích của hình trên bao gồm diện tích 2 nữa hình tròn bán kính r =7 cm và diện tích của hình chữ nhật kích thước 10×7 cm.

Câu 6: Tính S hình tròn, biết nếu tăng đường kính đường tròn lên 30% thì DT hình tròn tăng thêm 20 cm2
Giải: Nếu tăng đường kính của hình tròn lên 30% thì bán kính cũng tăng 30%
Số % S(diện tích) được tăng thêm là:
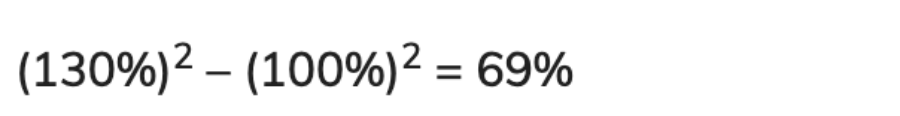
Vậy diện tích hình tròn ban đầu là: 20×100/69 = 29,956 cm2
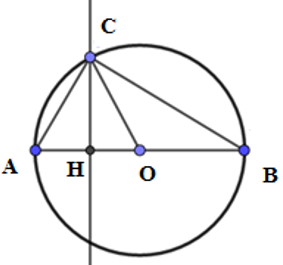
Câu 7: Cho hình vuông có cạnh 5cm nội tiếp đường tròn (O). Hãy tính độ dài đường tròn (O) và diện tích hình tròn (O).
Lời giải:
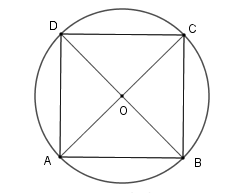
Gọi hình vuông nội tiếp đường tròn (O) là ABCD khi đó:
Xét tam giác ABC vuông tại B ta có:
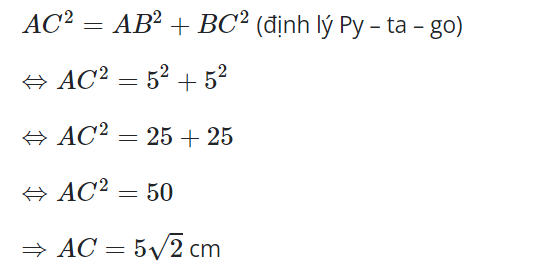
Vậy bán kính đường tròn là:
Chu vi đường tròn là:
Diện tích hình tròn là:
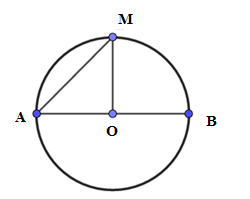
Câu 8: Cho đường tròn (O, 10 cm) , đường kính AB. Điểm M ∈ (O) sao cho
Tính diện tích hình quạt AOM.
Lời giải:

Câu 9: Biết rằng độ dài cung tròn có số đo 60° là π. Tính diện tích hình quạt tròn có số đo 30°
A. 2π
B. 4π
C. 5/2 π
D. 3/2 π
Lời giải:
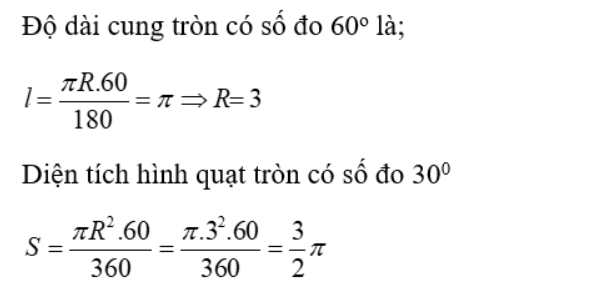
Chọn đáp án D.
Câu 10: Biết diện tích hình quạt cung n° là 120 . Tính diện tích hình quạt của cung 2n°?
A. 240
B.120
C. 480
D. 360
Lời giải:

Chọn đáp án A.
Câu 11: Một hình quạt có chu vi bằng 28 (cm) và diện tích bằng 49 (cm2). Bán kính của hình quạt bằng?
A. R = 5 (cm)
B. R = 6 (cm)
C. R = 7 (cm)
D. R = 8 (cm)
Lời giải:
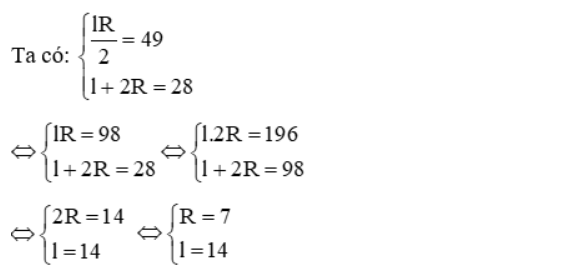
Vậy R = 7 (cm)
Đáp án cần chọn là: C
Câu 12: Cho đường tròn (O) đường kính AB = 2√2 cm. Điểm C ∈ (O) sao cho
= 30°. Tính diện tích hình giới hạn bởi đường tròn (O) và AC, BC
Lời giải:



Đáp án cần chọn là: A
2. Bài tập tính diện tích hình tròn không có lời giải
Câu 1: Tính diện tích của hình tròn có bán kính bằng 3cm.
Câu 2: Tính diện tích của hình tròn biết đường kính bằng 16m.
Câu 3: Một hình tròn có chu vi bằng 18,584cm. Tính diện tích của hình tròn đó.
Câu 4: Một hình tròn có chu vi bằng 8,42 dm. Tính diện tích của hình tròn đó.
Câu 5: Tính diện tích hình tròn biết độ dài đường kính bằng độ dài cạnh hình vuông có chu vi bằng 30cm.
Câu 6: Tính diện tích hình tròn biết độ dài bán kính bằng chiều rộng của hình chữ nhật có chu vi bằng 30cm và chiều dài bằng 12cm.
Trên đây là công thức diện tích hình Tròn & cách tính diện tích hình Tròn đơn giản mà đội ngũ INVERT chúng tôi đã tổng hợp được. Mong rằng thông qua bài viết này các bạn có thể tính được diện tích hình Tròn một cách dễ dàng.
