Tập hợp số là một khái niệm vô cùng quen thuộc với chúng ta từ lớp 6 ngay từ bài đầu tiên với những tập hợp số tự nhiên, số nguyên cũng như số hữu tỉ, số vô tỉ, số thực dương nằm ở trong chương trình toán cấp THCS. Hôm nay, chúng ta sẽ tiếp tục được làm quen với tập hợp số ở chương đầu toán THPT lớp 10. Vậy có bao nhiêu loại tập hợp số trong toán học, mối quan hệ giữa các tập hợp số cũng như các phép toán tập hợp số, chúng ta hãy cùng tìm hiểu ở bài viết dưới đây nhé!
1. Các loại tập hợp số trong toán học
Ở phần tập hợp số lớp 10, ta được học tất cả là bốn tập hợp số, đó chính là:
– Tập hợp của các số tự nhiên được quy ước kí hiệu là N: N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,…}.
– Tập hợp của các số nguyên được quy ước kí hiệu là Z: Z={…, -4, -3, -2, -1, 0, 1, 2, 3, 4, …}. Còn đối với số nguyên dương, tập hợp được kí hiệu là N*.
– Tập hợp của các số hữu tỉ, được quy ước kí hiệu là Q: Q = {1,2; 2,3; 3,4;…}. Một số hữu tỉ có thể được biểu hiện bằng số thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn.
– Tập hợp của các số thực được quy ước kí hiệu là R: Nếu số là số thập phân vô hạn không tuần hoàn thì ta gọi đó là số vô tỉ, tập hợp của số đó được kí hiệu là I. Còn tập hợp của số thực bao gồm số vô tỉ và số hữu tỉ.
2. Mối quan hệ giữa các tập hợp số
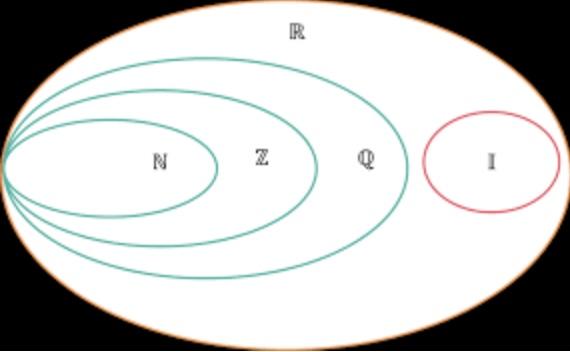
Hình minh họa mối quan hệ tập hợp số
Dựa trên mối quan hệ của các tập hợp số, ta có: R = Q ∪ I.
Tập N ; Z ; Q ; R.
Khi đó quan hệ bao hàm giữa các tập hợp số là: N ⊂ Z ⊂ Q ⊂ R
Nếu biểu thị qua biểu đồ thì ta sẽ được như trên hình.
3. Các phép toán trong tập hợp số của toán học
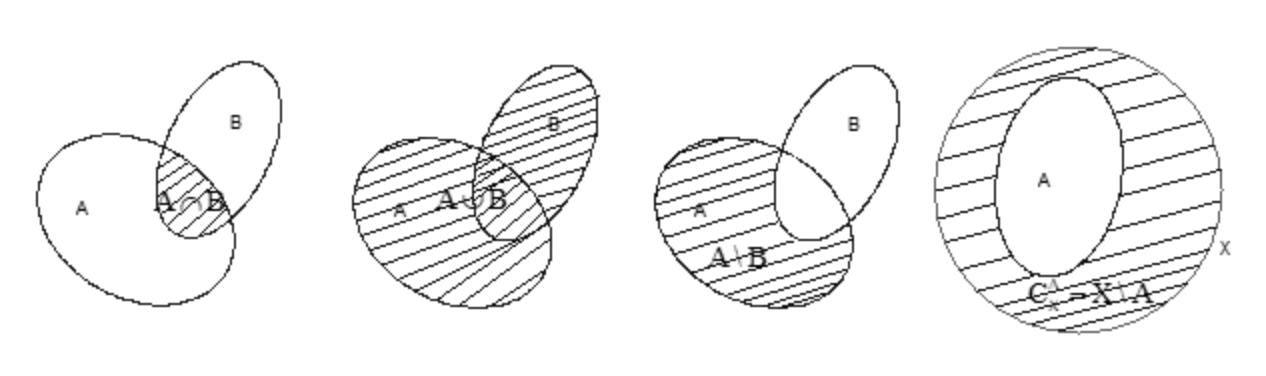
Minh họa các phép toán trong tập hợp số của toán học
Phép hợp
Hợp của hai tập hợp A và B, ký hiệu là A ∪ B, là tập hợp bao gồm tất cả các phần tử thuộc A hoặc thuộc B.
A ∩ B⇔{x ∣ x ∈ A và x ∈ B}
- Ví dụ: Cho tập A = {2;3;5}, B = {1;2} thì A∪B = {1;2;3;5}
Phép giao
Giao của hai tập hợp A và B, kí hiệu: A ∩ B. Là tập hợp bao gồm tất cả các phần tử thuộc cả A và B.
A∪B⇔{x ∣ x ∈ A hoặc x ∈ B}
Nếu 2 tập hợp A và B không có phần tử chung, nghĩa là A∩B = ∅ thì ta gọi A và B là 2 tập hợp rời nhau.
- Ví dụ: Cho tập A = {2;3;4}, B = {1;2} thì A∩B = {1}
Phép hiệu
Là hiệu của tập hợp A và B là tập hợp tất cả các phần tử thuộc A nhưng không thuộc B, ký hiệu: A∖B
A∖B = x∣x ∈ A và x ∉ B
- Ví dụ: Cho tập A = {2;3;4}, B = {1;2} thì:
- A∖B = {3;4}
- B∖A = {1}
Phép lấy phần bù
Cho A là tập con của tập E. Phần bù của A trong X là X∖A, ký hiệu là CxA là tập hợp cả các phần tử của E mà không là phần tử của A.
- Ví dụ: Cho tập A = {2;3;4}, B = {1;2} thì CAB = A∖B = {3;4}
4. Bài tập ví dụ có lời giải
Câu 1: Cho tập hợp Khẳng định nào sau đây đúng?
A. B. C. D.
Câu 2: Cho tập hợp Khẳng định nào sau đây đúng?
A. . B. . C. . D. .
Câu 3: Cho tập hợp Khẳng định nào sau đây đúng?
A. B. C. D.
Câu 4: Cho và . Xác định
A. B. C. D.
Câu 5: Cho và Gọi Khẳng định nào sau đây đúng?
A. B.
C. D.
Câu 6: Cho các số thực thỏa . Khẳng định nào sau đây đúng?
A. B.
C. D.
Câu 7: Cho hai tập hợp và Có bao nhiêu số tự nhiên thuộc tập ?
A. B. C. D.
Câu 8: Khẳng định nào sau đây sai?
A. B. C. D.
Câu 9: Cho tập hợp . Khẳng định nào sau đây đúng?
A. B. C. D.
Câu 10: Cho và . Xác định
A. B.
C. D.
ĐÁP ÁN
Câu 1 2 3 4 5 6 7 8 9 10 ĐA D A B D D A C D B C
Lời giải
Câu 1. Chọn D.
Câu 2. Chọn A.
Câu 3. Xét các đáp án:
• Đáp án A. Ta có .
• Đáp án B. Ta có .
• Đáp án C. Ta có .
• Đáp án D. Ta có là tập hợp các số hữu tỉ trong nửa khoảng .
Chọn B.
Câu 4. Ta có . Chọn D.
Câu 5. Ta có . Chọn D.
Câu 6. Chọn A.
Câu 7. Ta có:
Suy ra có hai số tự nhiên là và Chọn C.
Câu 8. Chọn D. Câu 9. Chọn B. Câu 10. Chọn C.
Trên đây là toàn bộ kiến thức về tập hợp số lớp 10. Nếu nắm vững được kiến thức này sẽ giúp các em có quá trình học đại số tốt hơn, có thể giải được nhiều bài toán khó liên quan đến tập hợp như tìm tập xác định của một hàm số, hay kết luận tập nghiệm của một bất phương trình. Rất mong bài viết này sẽ giúp các em nắm vững các tập hợp số, biết cách giải một số câu hỏi toán trắc nghiệm để có thể tích lũy kiến thức cho kì thi THPT nhé!