I. Khái niệm về Hình thoi
Hình thoi trong hình học Euclide là tứ giác có bốn cạnh bằng nhau. Từ khái niệm, ta thấy: ABCD là hình thoi => AB = BC = CD = DA
II. Tính chất của Hình thoi
Hình thoi cũng là một hình bình hành, nên nó có tất cả các tính chất của hình bình hành.
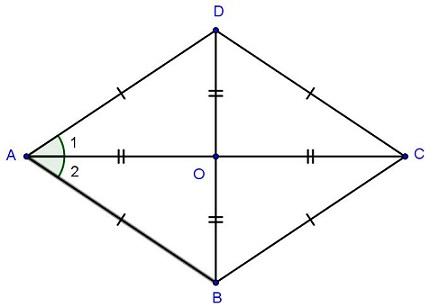
– Tính chất 1: Trong hình thoi, các góc đối nhau bằng nhau.
Dựa vào khái niệm về hình thoi, ta có:
∆ABC = ∆ADC (c .c. c) => Góc B = Góc D
∆ABD = ∆CBD (c .c .c) => Góc A = Góc C
– Tính chất 2: Trong hình thoi, hai đường chéo là các đường phân giác của các góc của hình thoi.
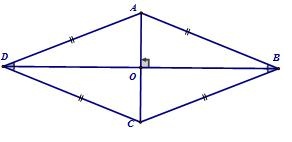
Xét ∆AOB và ∆COB có:
Chung cạnh OBOA = OC (O là trung điểm AC, do ABCD cũng là một hình bình hành)BA = BC (Hinh thoi có 4 cạnh bằng nhau)
Suy ra ∆AOB = ∆COB (c. c. c)
=> Góc ABO = Góc CBO => BO hay BD là đường phân giác của Góc ABC và Góc ADC
Chứng minh tương tự, ta cũng có: AC là đường phân giác của Góc BAD và Góc BCD
– Tính chất 3: Trong hình thoi, hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
Xét ∆BAD cân tại A có AO là đường phân giác ứng với góc Â
=> AO đồng thời cũng là đường cao ứng với BD
=> AO ⊥ BD
=> Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
III. Các cách chứng minh tứ giác là Hình thoi
Cách 1: Tứ giác có bốn cạnh bằng nhau
Ví dụ: Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của hình thoi.
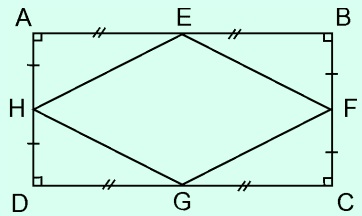
Xét tam giác ABD có E và H lần lượt là trung điểm của AB và AD
=> EH là đường trung bình của tam giác
=> EH = 1/2 BD (1)
Chứng minh tương tự ta có: EF = 1/2 AC; FG = 1/2 BD; HG = 1/2 AC (2)
Vì ABCD là hình chữ nhật nên AC = BD (3)
Từ (1), (2) và (3), ta suy ra EH = EF = HG = GF
=> Tứ giác EFGH là hình thoi do có bốn cạnh bằng nhau. (đ.p.c.m)
Cách 2: Tứ giác có 2 đường chéo là đường trung trực của nhau
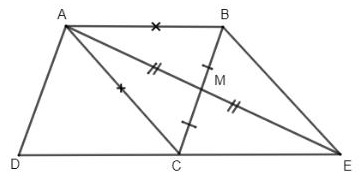
Ví dụ: Cho hình bình hành ABCD có AB = AC. Kéo dài trung tuyến AM của ΔABC và lấy ME = MA. Chứng minh tư giác ABEC là hình thoi.
Theo bài ra, ta có:
ΔABC cân tại A có trung tuyến AM
=> AM đồng thời là đường trung trực của BC
=> Tứ giác ABEC là hình thoi do có 2 đường chéo là đường trung trực của nhau. (đ.p.c.m)
Cách 3: Hình bình hành có hai cạnh kề bằng nhau
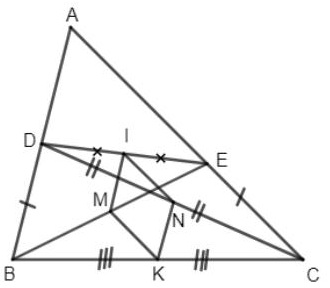
Ví dụ: Cho tam giác ABC, lấy các điểm D, E theo thứ tự trên các cạnh AB, AC sao cho BD = CE. Gọi M, N, I, K lần lượt là trung điểm của BE, CD, DE, BC. Chứng minh rằng: IMNK là hình thoi.
Theo giả thiết ta có: M là trung điểm của BE và I là trung điểm của DE
=> MI là đường trung bình của ΔBDE
=> MI // BD và MI = 1/2 BD
Chứng minh tương tự, ta có:
NK // BD và NK= 1/2 BD
Do có MI // NK và MI = NK nên tứ giác MINK là hình bình hành (4)
Chứng minh tương tự, ta có: IN là đường trung bình của ΔCDE
=> IN = 1/2 CE mà CE = BD (gt) => IN = IM (5)
Từ (4) và (5) => Tứ giác MINK là hình thoi do là hình bình hành có hai cạnh kề bằng nhau. (đ.p.c.m)
Cách 4: Hình bình hành có hai đường chéo vuông góc
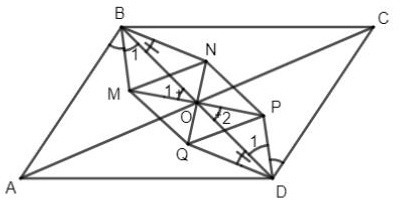
Ví dụ: Gọi O là giao điểm hai đường chéo của hình bình hành ABCD. Chứng minh rằng giao điểm các đường phân giác trong của các tam giác AOB; BOC; COD và DOA là đỉnh của một hình thoi.
Gọi M, N, P, Q lần lượt là giao điểm các phân giác trong của các tam giác AOB, BOC, COD và DOA.
Do O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD nên OA = OC và OB = OD.
Xét ΔBMO và ΔDPO có:
Góc B1 = D1 và Góc O1 = O2 ( đối đỉnh ) và OB = OD (gt)
=> ΔBMO = ΔDPO (g. c. g)
=> OM = OP và các điểm M, O, P thẳng hàng (6)
Chứng minh tương tự: ON = OQ và N, O, P thẳng hàng (7)
Từ (6) và (7) Suy ra: Tứ giác MNPQ là hình bình hành do các đường chéo cắt nhau tại trung điểm mỗi đường. (8)
Mặt khác OM, ON là hai đường phân giác của hai góc kề bù nên OM ⊥ ON. (9)
Từ (8) và (9) suy ra: MNPQ là hình thoi do là hình bình hành có hai đường chéo vuông góc. (đ.p.c.m)
Mọi người cũng hỏi
Câu hỏi 1: Làm thế nào để chứng minh một hình thoi?
Trả lời 1: Để chứng minh một hình thoi, bạn có thể sử dụng các phương pháp như chứng minh các đỉnh đối diện bằng nhau, chứng minh hai đoạn chéo vuông góc nhau, hay sử dụng tính chất cạnh và góc của hình thoi.
Câu hỏi 2: Tính chất cơ bản của hình thoi là gì?
Trả lời 2: Hình thoi là một tứ giác có cả bốn cạnh bằng nhau và hai góc đối diện bằng nhau. Nó cũng có hai đoạn chéo vuông góc nhau tại trung điểm của chúng.
Câu hỏi 3: Làm thế nào để chứng minh rằng hai đoạn chéo trong hình thoi vuông góc nhau?
Trả lời 3: Để chứng minh rằng hai đoạn chéo trong hình thoi vuông góc nhau, bạn có thể sử dụng tính chất của đoạn chéo chia tứ giác thành hai tam giác vuông cân và chứng minh rằng các góc của các tam giác vuông cân đối diện với nhau.
Câu hỏi 4: Có bao nhiêu cách để chứng minh một hình thoi?
Trả lời 4: Có nhiều cách để chứng minh một hình thoi, tùy thuộc vào thông tin và điều kiện đã cho. Một số cách thường được sử dụng là chứng minh các cạnh và góc bằng nhau, chứng minh tính chất của đoạn chéo và góc trong hình thoi.
